Question: May i know the solution to this? Let X1, . . . ,Xn be an i.i.d. sample from the uniform distribution on [0 1, 0
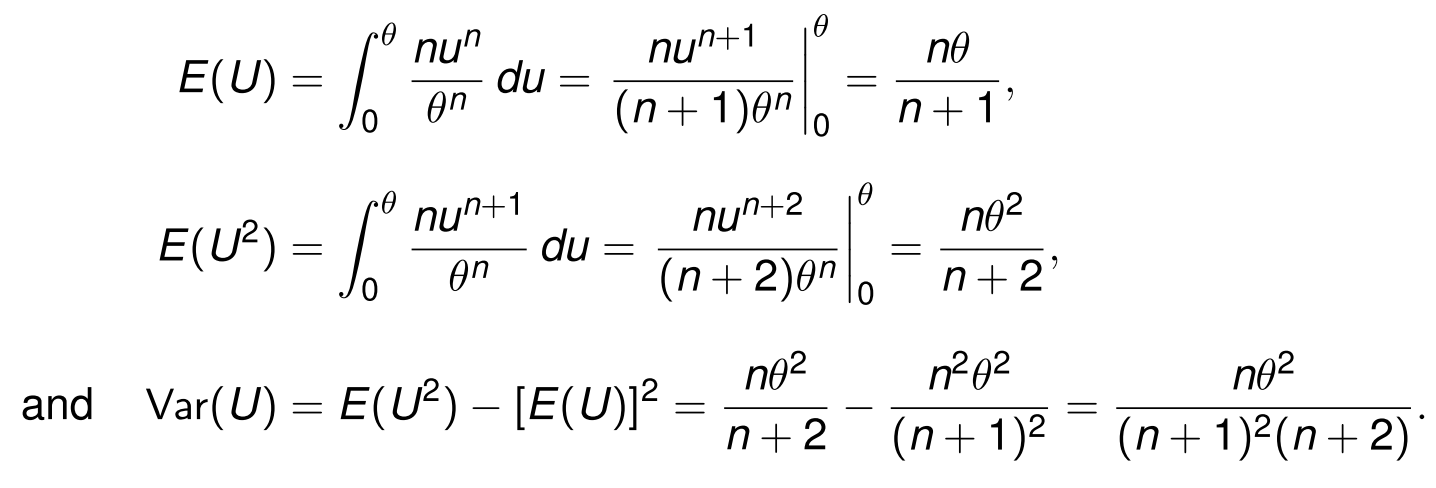
May i know the solution to this?

![1, 0 + 1]. With U = maX{X1, . . . ,Xn}](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6678ac373818d_4396678ac371c360.jpg)
Let X1, . . . ,Xn be an i.i.d. sample from the uniform distribution on [0 1, 0 + 1]. With U = maX{X1, . . . ,Xn} and V = min{X1, . . . ,Xn}, any value between U 1 and V + 1 is an mle for 0. In particular, consider A (U1)+(V+1) U+V 1=U1 and 62=+= 2 . 1. Find the bias, the variance, and the mean squared error of 51. Hint: Let Y,- = {X,- (0 1)}/2. Then Y1, . . . ,Yn are i.i.d. uniform on [0,1]. The mean and variance of max{Y1, . . . , Yn} are given by Problem 20 (with 0 = 1). 2. Find the bias, the variance, and the mean squared error of g. Hint: The density function of dz is H )_{(n/2){x(01)}"'1, 01930, \"3 _ (n/2){(0+1)$}"_1, 0930\". 0 nun nun+1 E(U = du = 0 on (n + 1 )on 0 n+ 1 0 nun+1 nun+2 E(US) = no2 du = 0 on (n + 2)on 0 n+2 and Var(U) = E(U2) - [E(U)12 = 1202 no2 n+ 2 ( n + 1 ) 2 (n+ 1)2(n+ 2)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


