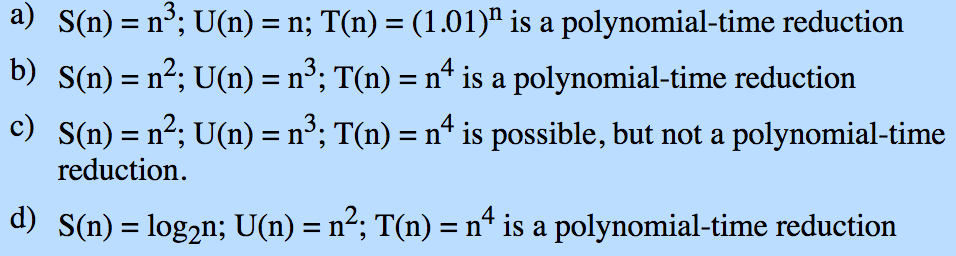MCQ:

A)

There is a Turing transducer T that transforms problem P1 into problem P2. T has one read-only input tape, on which an input of length n is placed. T has a read-write scratch tape on which it uses O(S(n)) cells. T has a write-only output tape, with a head that moves only right, on which it writes an output of length O(U(n)). With input of length n, T runs for O(T(n)) time before halting. You may assume that each of the upper bounds on space and time used are as tight as possible.

A given combination of S(n), U(n), and T(n) may:

1. Imply that T is a polynomial-time reduction of P1 to P2.

2. Imply that T is NOT a polynomial-time reduction of P1 to P2.

3. Be impossible; i.e., there is no Turing machine that has that combination of tight bounds on the space used, output size, and running time.

What are all the constraints on S(n), U(n), and T(n) if T is a polynomial-time reducer? What are the constraints on feasibility, even if the reduction is not polynomial-time? After working out these constraints, identify the true statement from the list below.

-

B)

The Boolean expression wxyz+u+v is equivalent to an expression in 3-CNF (a product of clauses, each clause being the sum of exactly three literals). Find the simplest such 3-CNF expression and then identify one of its clauses in the list below. Note: -e denotes the negation of e. Also note: we are looking for an expression that involves only u, v, w, x, y, and z, no other variables. Not all boolean expressions can be converted to 3-CNF without introducing new variables, but this one can.

(a)

(w+z+u)

(b)

(y+z+v)

(c)

(x+y+v)

(d)

(z+u+v)

S(n) n", UiOn) n; Tn) (1.01) is a polynomial-time reduction b) S(n)- n2; U(n) ns; T(n) n is a polynomial-time reduction c) S(n) n2, U(n) n3; Tn) n4 is possible, but not a polynomial-time reduction. d) S(n) log2n; U(no 2. T(n) n is a polynomial-time reduction S(n) n", UiOn) n; Tn) (1.01) is a polynomial-time reduction b) S(n)- n2; U(n) ns; T(n) n is a polynomial-time reduction c) S(n) n2, U(n) n3; Tn) n4 is possible, but not a polynomial-time reduction. d) S(n) log2n; U(no 2. T(n) n is a polynomial-time reduction