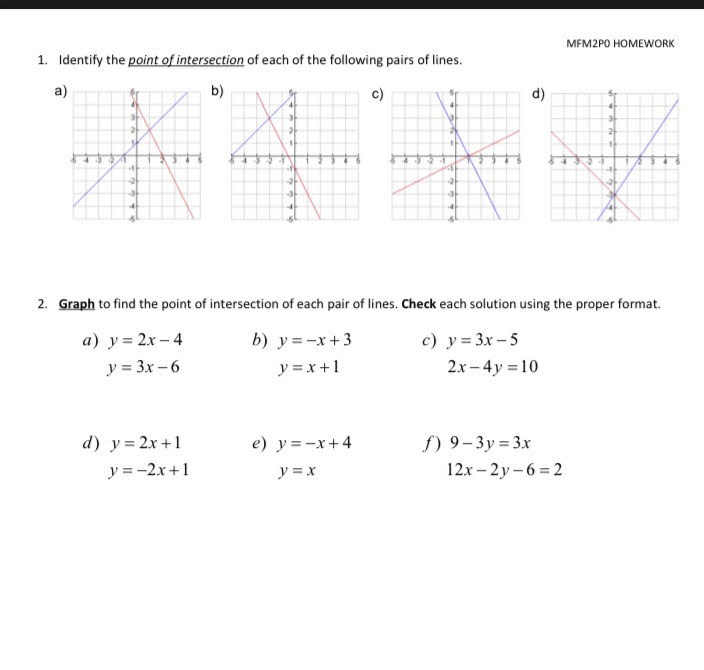
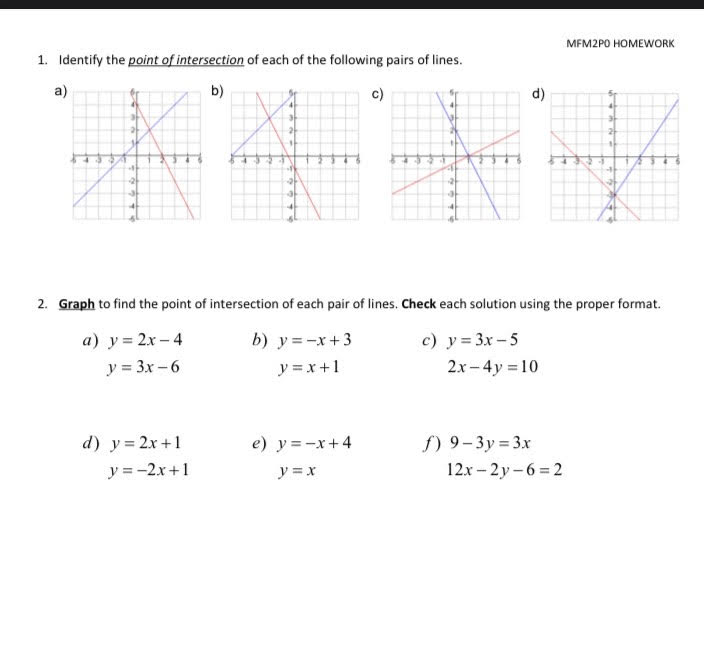
MFM 2P Name: Unit 2: Linear Systems Date: 4.2 Solving Linear Systems by Substitution, pt 1 STEPS: 1. Make sure one of the equations is solved for one of the variables. 2. Substitute the solved equation into the other equation and solve for the unknown value. 3. Substitute the value found in STEP 2 into the first equation and solve for the unknown value. 4. The point of intersection is made up of the co-ordinates found in STEPS 2 & 3. Example: Determine the point of intersection of the following systems: a) y=-x+6 2x - y = 0 STEP 3: Substitute into equation 1: STEP 1: Equation is already solved for STEP 2: Substitute in for y in equation 2: STEP 4: The point of intersection is b) 3x + 18y = 12 x = -3y+1 STEP 3: Substitute into equation 2: STEP 1: Equation is already solved for STEP 2: Substitute in for x in equation 1: STEP 4: The point of intersection isMFM 2P Name: Unit: Linear Systems Date: 4.1 Solving a System of Equations by Graphing of linear equations consists of two or more linear equations. When graphed, the represents the to the system of linear equations. The for the point of intersection must satisfy each equation in the system. Example: Find the solution to the following system of equations by graphing both lines. Line A: x + y = 6 Line B: 2x - y = 0 10 STEP 1: Re-arrange both equations into y = mx + b form. 8 6 10 8 6 4 -2 2 4 6 8 10 STEP 2: Graph both lines carefully on the same grid using the slope and y-intercept method. STEP 3: Find the point of intersection of the two lines on the graph. From the above graph, the point of intersection appears to be STEP 4: Check the point in both equations using a formal LS = RS check. Line A: x + y = 6 Line B: 2x - y = 0 LS RS LS RS STEP 5: If the point satisfies both equations, then it is the solution. If the point does not satisfy both equations, then go back and check your work. "LS = RS for both equations, point satisfies both equations. . . Point is the solution to the system.MFM2PO HOMEWORK On a separate piece of paper, answer the following questions: 1. Solve for y. You only need to ISOLATE in these questions (get y by itself on one side of the equation). a)y+ 7x =12 b)- 4x+y=-9 2. Solve for x. You only need to ISOLATE in these questions (get x by itself on one side of the equation). a) x+3y =7 b)8y-x=-4 3. Solve each linear system by substitution. Use the examples from the video to know how to show your work. a)y = 3x +5 b) y = 2x -7 c)x = 3y+8 4x -3y =-25 3x + y=-17 xty =-2 d)- x - 3y =5 e) 3x - 2y = -4 3 f)y=-13-4x y = - -X 4 x =-2+2y 3x - 4y =14 g)x+ 6y=-11 h)4x -7y =20 i)7x- y-13=0 -7x+3y =-13 x - 3y =10 -4x -9y =-17MFM2PD HOMEWORK 1. Identify the point of intersection of each of the following pairs of lines. a) b) c) d) 2. Graph to find the point of intersection of each pair of lines. Check each solution using the proper format. a) y = 2x -4 b) y=-x+3 c) y = 3x - 5 y = 3x -6 y= x+1 2x -4y =10 d) y = 2x+1 e) y=-x+4 f) 9-3y =3x y =-2x+1 V= x 12x -2y-6 =2