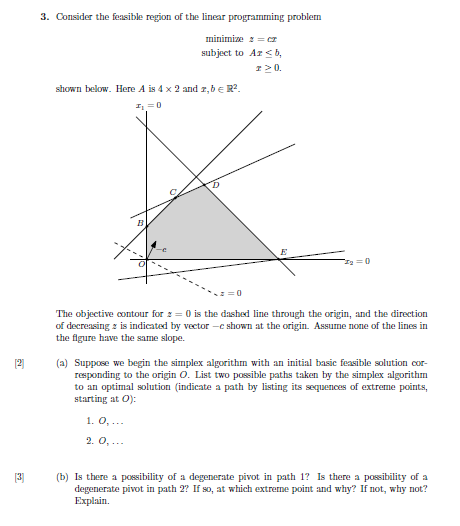
Midterm Exam Math 308 Fall, 2013 Simon Fraser University D. Funk Pertinent info: 1. To receive full credit for a particular question you must provide a complete and well presented solution. 2. This exam has 8 questions on 4 pages. Please check to make sure your exam is complete. 3. No books, papers, or electronic devices are permitted. A basic scientific calculator is unnecessarily permitted. RHS C.BON - GN How 0 A b Rows I through me [5) 1. A television manufacturer has to decide on the number of L.C.D. and C.R.T. TV's to produce. Market research indicates that at most 30100 units of L.C.D.s and at most 4000 units of C.IT.s can be sold each month. The maximum number of man-hours available is 70,000 per month. An L.C.D. TV requires 20 man-hours and a C.R.T. requires 15 man-hours to manufacture. The unit profits of the L.C.D. and C.R.T. TV's are $60 and $40, respectively. Formulate the problem of determining how many units of each TV type should be produced in order to maximize profit as a linear program. [5) 2. Show that the set of all feasible solutions to the linear program minimize er subject to Ax = b, is a convex set.3. Consider the feasible region of the linear programming problem minimize = = CT subject to Ar