Question: Minimum Vertex Cover Problem: 1A) Choose a simple and connected Graph G1 with 8 nodes such that MIN(VC) with (G1,2) as input has a negative
Minimum Vertex Cover Problem:
1A)
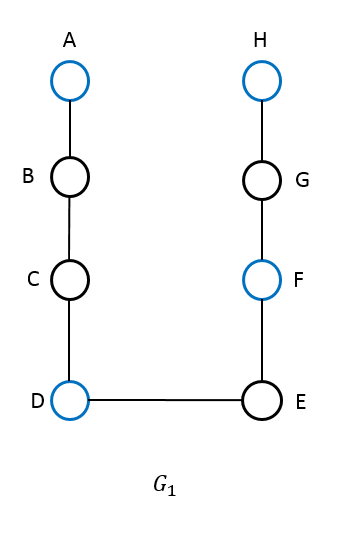
Choose a simple and connected Graph G1 with 8 nodes such that MIN(VC) with (G1,2) as input has a negative solution, i.e. there not exists a cover 2 Explain Why does not exist a cover such that |Vcmin|2; |Vc| is the cardinality of V. I choose the Graph in figure.
1B)
Choose a simple and connected Graph G2 with 6 nodes such that MIN(VC) with (G2,3) as input has a negative solution, i.e. there not exists a cover 3 Explain Why does not exist a cover such that |Vcmin|3; |Vc| is the cardinality of V. Write the Graph and evidence the cover.
1
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


