Question: MnSi has a simple cubic structure. The figure below shows the diffracted X-ray intensity from a single crystal film with its normal along the [111]
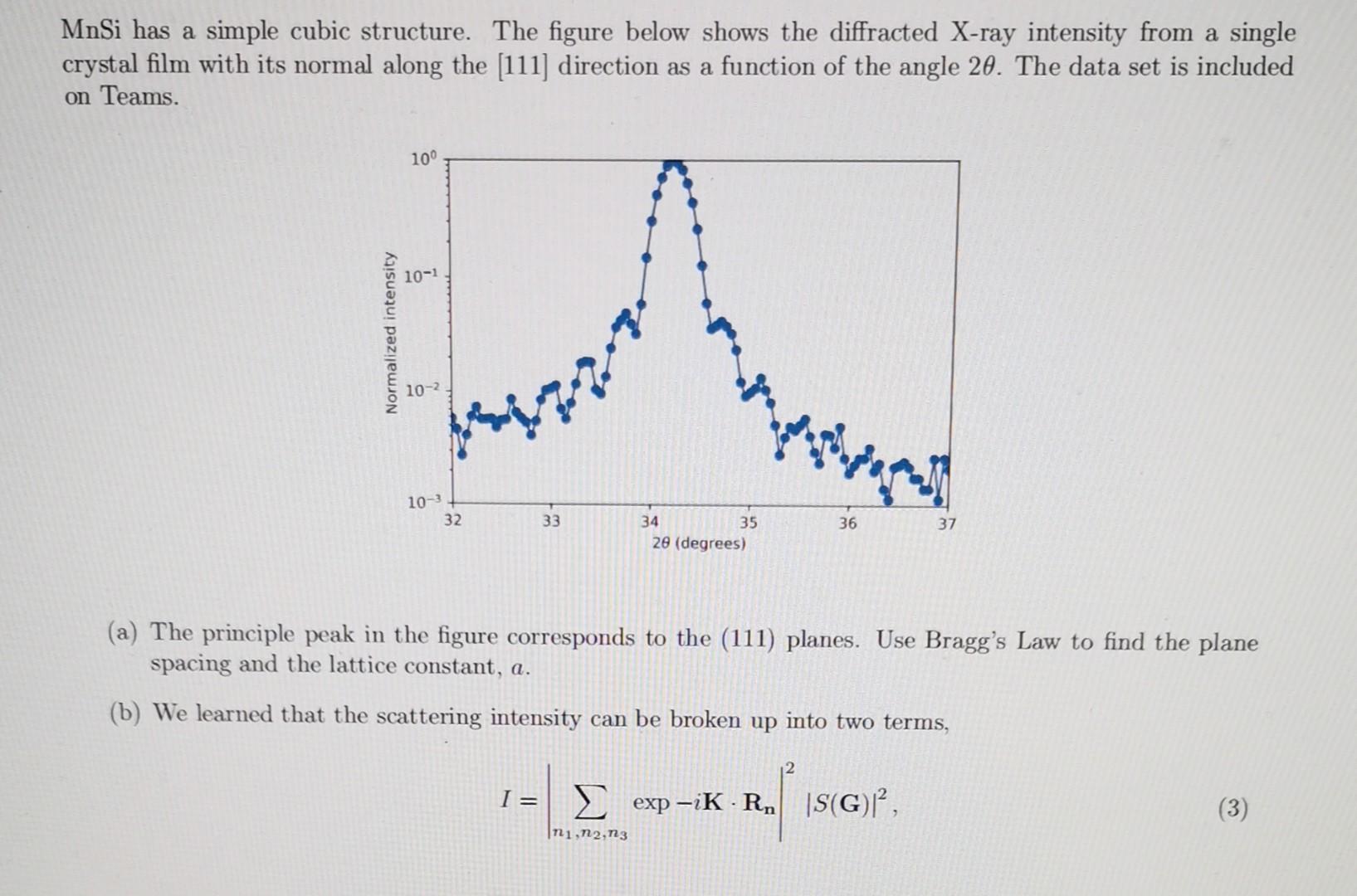

![the [111] direction as a function of the angle 2. The data](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66f92f033b276_53066f92f02d20fc.jpg)
MnSi has a simple cubic structure. The figure below shows the diffracted X-ray intensity from a single crystal film with its normal along the [111] direction as a function of the angle 2. The data set is included on Teams. (a) The principle peak in the figure corresponds to the (111) planes. Use Bragg's Law to find the plane spacing and the lattice constant, a. (b) We learned that the scattering intensity can be broken up into two terms, I=n1,n2,n3expiKRn2S(G)2 The second term is the structure factor. Ignore the structure factor S(G) in the following, as this is only important when comparing the relative intensities of the diffraction peaks. The first term is the geometric structure factor. Up until now, you have considered an infinite crystal. Here you will consider a thin MnSi film. For the experiment on the MnSi film, the instrument scanned K along the (111) direction. Show for this particular case that the scattering intensity in Eq. 3 becomes I=n=1Nexp(i3Kna)2, which is summed of over N atomic planes of the film. (c) Fit the data with the geometric structure factor. From your fit, determine the thickness of the film. You can use the geometric series you used in Problem Set 2 to simplify Eq. 4 (or simply sum the exponentials numerically). Hint: you need to relate the angle 2 in a X-ray diffraction experiment in terms of the magnitude of the scattering vector K. Your fit should capture the fringes about the main peak, but the calculated fringes are not as sharp as experiment, why? For Q3, use Lambda =1.5442^A (the wavelength of the Cu K-alpha radiation, which is widely used in the labs and the default setting in the VESTA powder diffraction tool). MnSi has a simple cubic structure. The figure below shows the diffracted X-ray intensity from a single crystal film with its normal along the [111] direction as a function of the angle 2. The data set is included on Teams. (a) The principle peak in the figure corresponds to the (111) planes. Use Bragg's Law to find the plane spacing and the lattice constant, a. (b) We learned that the scattering intensity can be broken up into two terms, I=n1,n2,n3expiKRn2S(G)2 The second term is the structure factor. Ignore the structure factor S(G) in the following, as this is only important when comparing the relative intensities of the diffraction peaks. The first term is the geometric structure factor. Up until now, you have considered an infinite crystal. Here you will consider a thin MnSi film. For the experiment on the MnSi film, the instrument scanned K along the (111) direction. Show for this particular case that the scattering intensity in Eq. 3 becomes I=n=1Nexp(i3Kna)2, which is summed of over N atomic planes of the film. (c) Fit the data with the geometric structure factor. From your fit, determine the thickness of the film. You can use the geometric series you used in Problem Set 2 to simplify Eq. 4 (or simply sum the exponentials numerically). Hint: you need to relate the angle 2 in a X-ray diffraction experiment in terms of the magnitude of the scattering vector K. Your fit should capture the fringes about the main peak, but the calculated fringes are not as sharp as experiment, why? For Q3, use Lambda =1.5442^A (the wavelength of the Cu K-alpha radiation, which is widely used in the labs and the default setting in the VESTA powder diffraction tool)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


