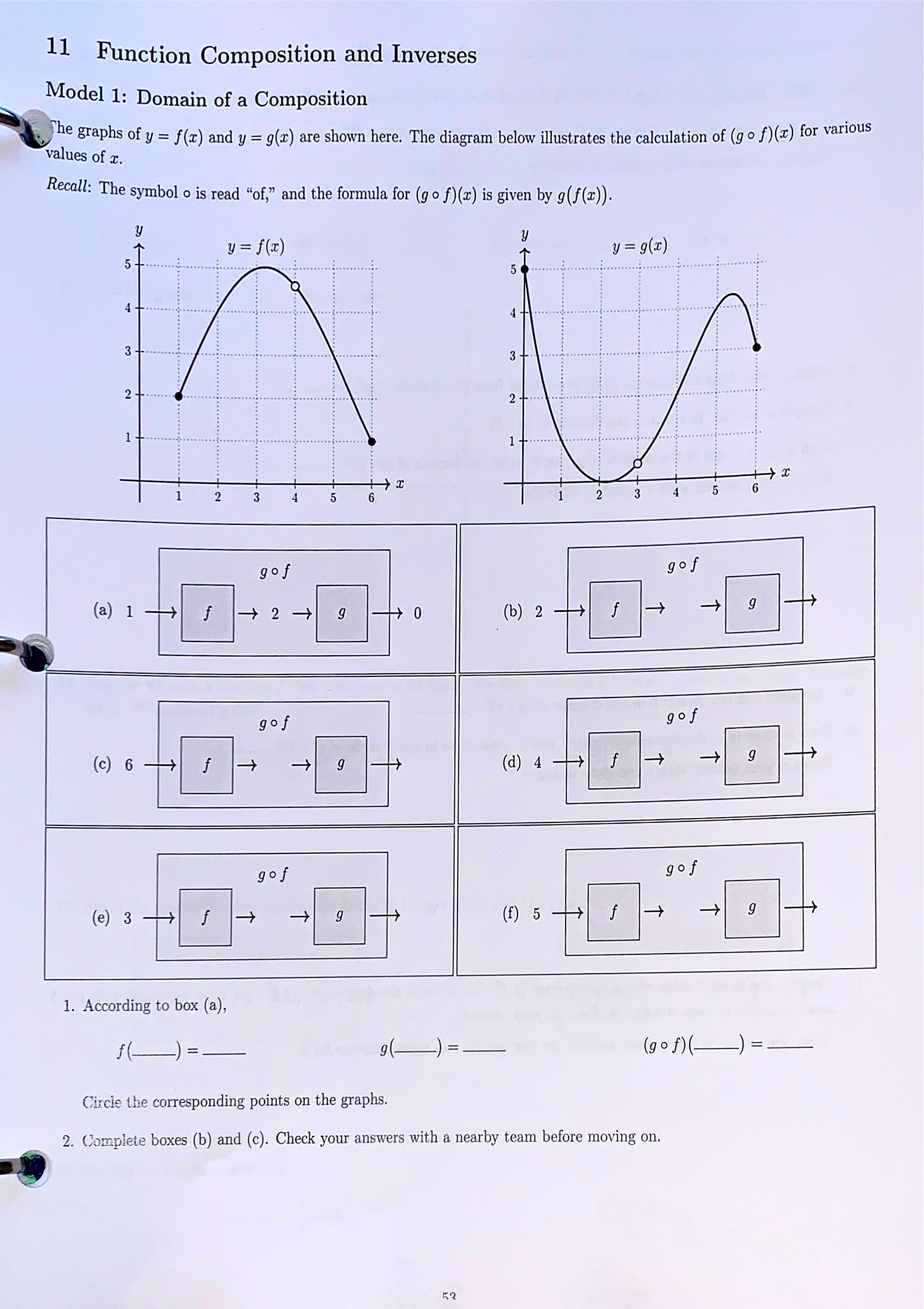
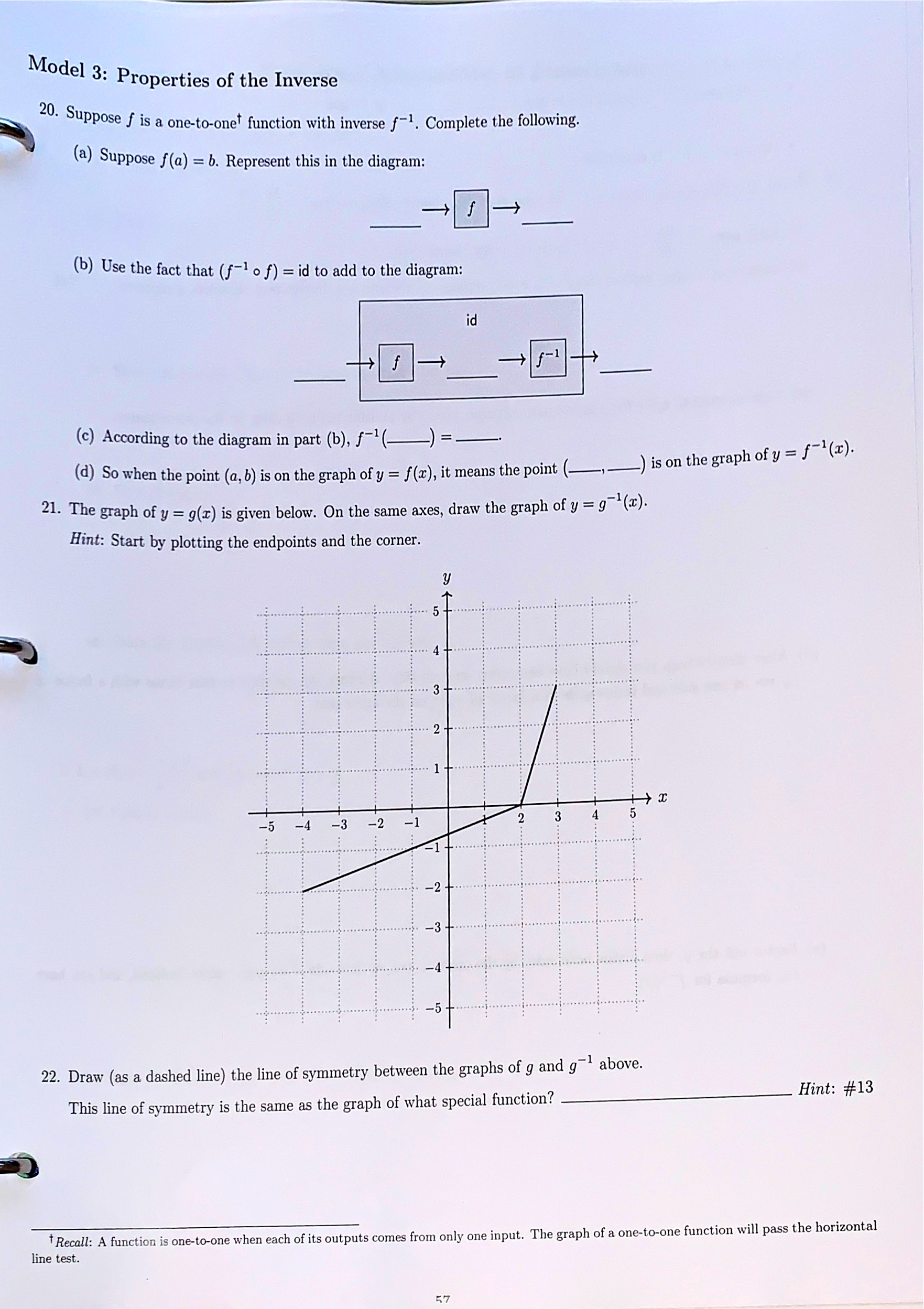
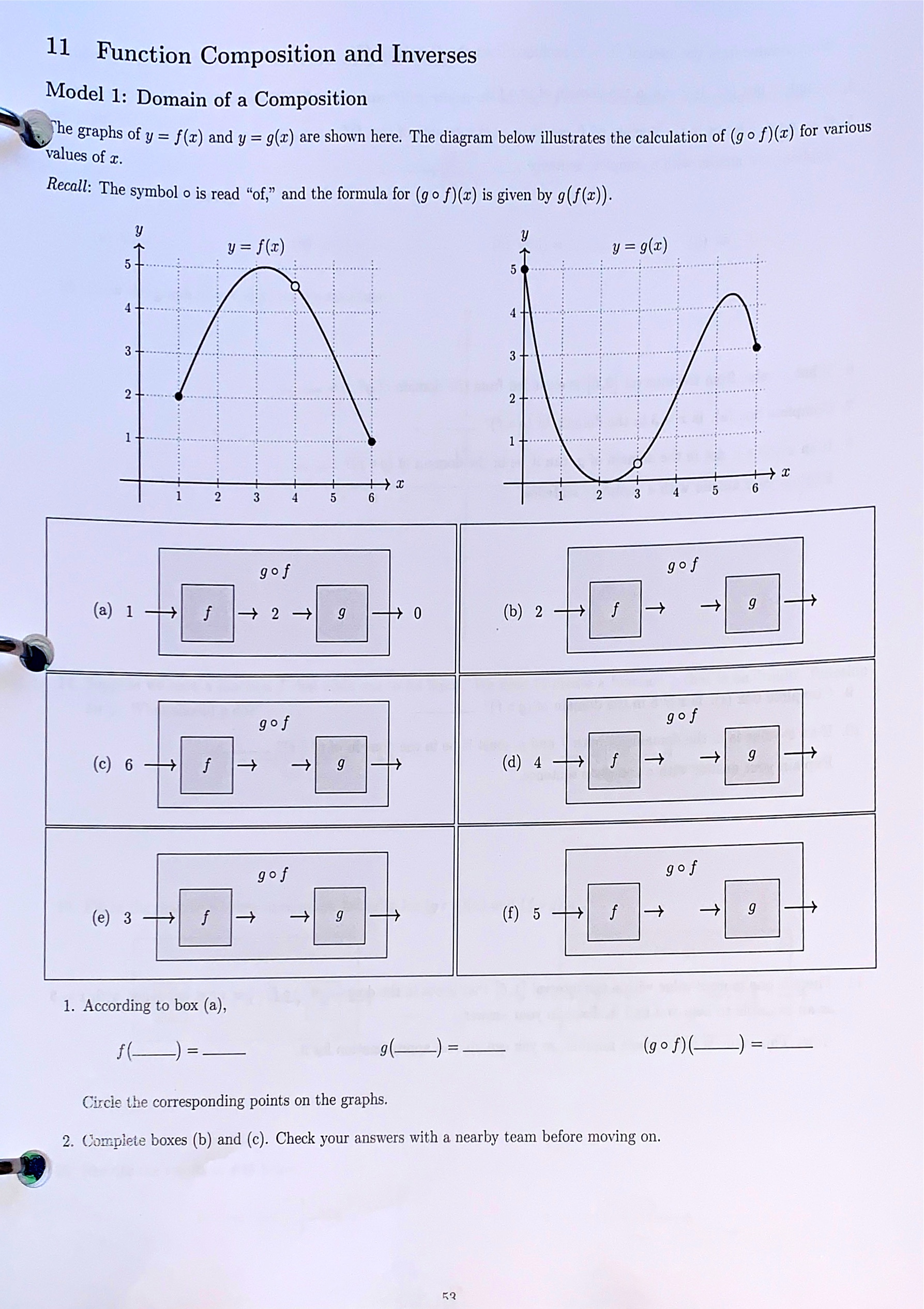
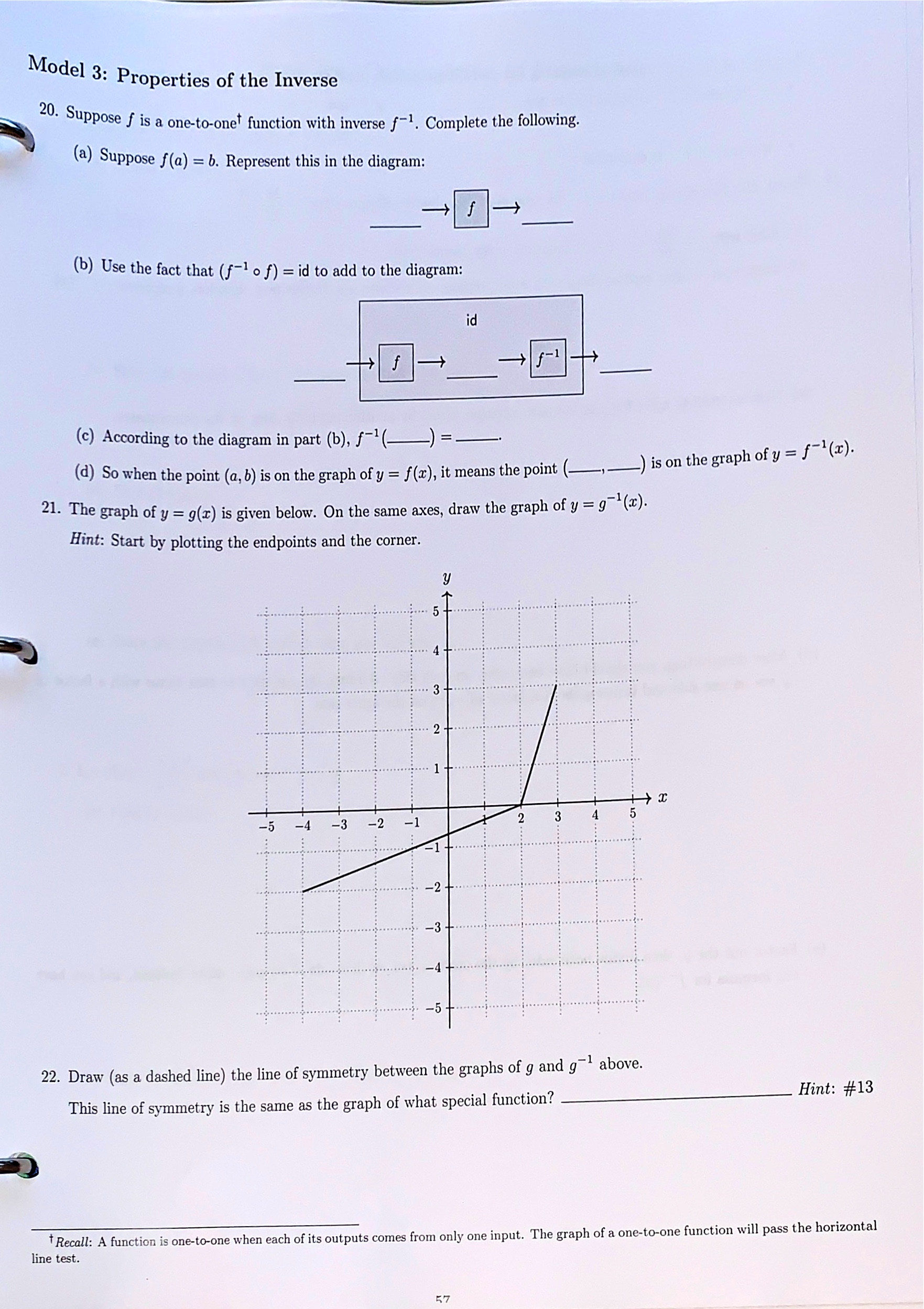
Model 3: Rational Inequalities First, recall an important fact about inequalities. Consider the true inequality, 5 > 3- f 14. Multiply both sides or the inequality by 2. Is it still true? __ \" 15. Multiply both sides of the inequality by 2. Is it still true? , ust be done to 16. In general, when multiplying (or dividing) both sides of an inequality by a negative number, What m make sure the truth of the inequality stays the same? Now, our goal is to solve the following inequality. x2 'rc3 - 2 d , nsidering . If this were a rational equation, we could multiply both sides by the common denominator, :1: (1' 3) C0 #16, why would this strategy be problematic for the inequality? Hint: Is 22(x - 3) positive or negative? 18. Instead. start by adding 2 to both sides of the inequality, so that zero is on the right side. . :c _ 19. Next, express the left side as a single fraction with a common denominator. It)? e 23. The graph or r1 f' TherEfor ' is obtained by Swapping the coordinates of each point on the graph or ' the domain OH"1 is equivalent, to the ._...._. 0f f9 and o the range of j"1 is equivalent to the - 0f f' 21: + 3 24. We can also nd the formula for f '1 by swapping coordinates. Suppose f (at) = airs" 2:1: + 3 71: _ 5. In this equation, 3; represents f (1:). (a) Start with y = 1 . , - e resents f (3)- (b) Swap coordinates: replace the y with a: and replace all art's with gas In \"1,5 new eQUation, y r P (c) Now we need to solve for y in the new equation. Start by multiplying both sides by the denominator' if . . . . . ' f (d) After distributing, you should have two terms on each Side. Arrange the equation so that terms With a factor 0 y are on one side and terms without a factor of y are on the other side. (9) Factor out the y, then divide both sides by the other factor on that side. Now y should be 1501\"\Practice: Composition of Functions 1. Let g(x) = 12 + 1 and let h(x) = VI + 6. (a) Evaluate (go h)(3). (b) Find (goh)(I). (c) State the domain of (go h)(x) using interval notation. (d) Find (hog)(I). (e) State the domain of (hog)(z) using interval notation. 2. Let f(z) = 2+6 r+ 3 and let g(x) = 2x + 3. (a) Find (fog)(I). (b) State the domain of (f o g)(r) using interval notation. 50Practice: Inverse Functions 3. Let m) = 3333. Find f'1(:c). 4- Let gm = 52+ 7. (a) Find 9%). (b) State the domain of g'1(x) using internal notation. (b) State the domain and range of h'1(a:) using interval notation. m 20. Fully factor both numerator and denominator and identify the zeros of each. Label them on the number line below along with their multiplicities. These numbers should split the r-axis into four intervals. signs zeros + mult. 21. Is the inequality true when the numerator is zero? If so, mark the zeros of the numerator as solid points on your number line above. Otherwise, mark them as open points. 22. Is the inequality true when the denominator is zero? If so, mark the zeros of the denominator as solid points on your number line above. Otherwise, mark them as open points. 23. Choose an r-value from one of the four intervals from #20, and plug it in to the fraction to see if it has a positive or negative value. Label that interval of the sign chart with a "+" or "-." 24. Use the multiplicities of the zeros to determine whether the sign of the fraction changes or does not change on either side of each zero. Use this information to fill in the rest of the signs. 25. The inequality is true when the fraction's value is either positive or zero. Write the set of x values for which the inequality is true as a union of intervals.Practice: Solving Rational Inequalities Solve the inequality. Graph the solution set on a number line and write the solution using interval notation. (Note: Your york must include number line reasoning.) 1. -1+5 50 2. 15 I+6 > 5\f11 Function Composition and Inverses MOdel 1: Domain of a Composition a Th - e graphs 0f y = f (I) and y = g(a:) are shown here. The diagram below illustrates the calculation of (g 0 f )(55) for var 'OUS values of 3:, Recall: The symbol 0 is read \"of,\" and the formula~ for (g o f )(z) is given by g( f (z)). y (:iZClE- the corresponding points on the graphs. 2. Complete boxes (b) and (c) Check your answers with a nearby team before moving on. _Q KQ 3. What r-value from the interval [1, 6] is excluded from the domain of f? I =. 4. Complete box (d). Is x = 4 in the domain of (go f)? 5. If an r-value is not in the domain of f, can it be in the domain of (go f)? Explain your answer with a complete sentence. 6. What r-value from the interval [0, 6] is excluded from the domain of g? I =. 7. Complete box (e). Is r = 3 in the domain of (go f)? 8. If an r-value is not in the domain of g, can it be in the domain of (go f)? Explain your answer with a complete sentence. 9. Complete box (f). Is a = 5 in the domain of (go f)? 10. If an r-value is in the domains of both f and g, must it be in the domain of (go f)? Explain your answer with a complete sentence. 11. There is one more r-value within the interval [1, 6] that is not in the domain of (go f). Use what happened with x = 5 as an example to help you find it. Explain your answer. Hint: This value is not a whole number, so you can give an approximation for it. 51Model 2: The Identity Function and Inverses was input: There is a special function called the identity function, which we denote by id. This function always outputs exactly what id 12. Evaluate the following. (a) id(0) = _ (b) id(1) = (c) id(3) = (d) id(-2) = - 13. Draw the graph of y = id(x) on the axes below. 2....... . ........) ..- 2 ..... ".... -4 -3 -2 -1 .... ..... i. . . . . . . . ...*. . -2 ...... -3 . .... -4+ .. S... 14. Suppose we have a function f that adds one to its input. We need to create a function g that is an "undo" function for f. What should g do? f + 2+1 9 15. Fill in the diagrams below to compute formulas for (go f)(r) and (fog)(x). (go f ) (fog) f + +1 9 g f 16. Rewrite the results of #15 below. x - (go f ) (fog)f0f_l) =1d and . Then the function f "1 is the inverse of f PTOVidEd that ( lies in the functions' domains. 19. Suppose f(:c) = 1'2 and g(:c) = fa}. (3) Recall from #12 that id(2) (b) Based on part (a), does (go f)=id? . ___ j 7 ((2) Based on part (b), is g the inverse of f? ((1) Suppose the domain of f is restricted to [0,00). On this domain, does (9 o f) = id? Explain your answer with a complete sentence. (e) Suppose the domain of f is instead restricted to (-oo,0]. How could you modify the formula for 9(33) so that g is the inverse of f on this domain? a: 19This problem illustrates why we need to include plus or minus when taking the square root of both sides of an equation. We are inverting a squaring function, but we don't know which inverse to use! RE Mod . 91 3. Properties of the Inverse 20. su . Ppose f 15 a oneto-oneT function with inverse f\". Complete the following- (3.) Suppose I (a) = b. Represent this in the diagram: '+ ('3) Use the fact that (f1 o f) = id to add to the diagram: (c) According to the diagram in part (h), f -1 () = -1 ) is on the graph Of 3/ = f (m). (d) 50 When the point (a, b) is on the graph of y = f (33). it means the point (' ' 21- The graph 0f y = 9(1) is given below. On the same axes, draw the graph 0f 31 = 94\") Hint: Start by plotting the endpoints and the corner. 1 above. 22. Draw (as a dashed line) the line of symmetry between the graphs of g and g ry is the same as the graph of what special function? ________'_ Hint: #13 This line of symmet ifRecall: A function is onetoone when each of its outputs comes from only one input. The graph of a one-to-one function will pass the horizontal line tat. R7