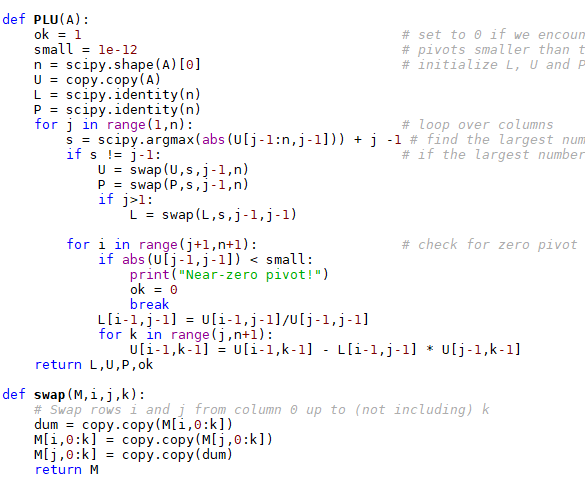
Modify the above python code so it computes an upper hessenberg matrix that avoids unnecessary FLOPS(i.e adding and multiplying by zero)

Upper Hessenberg matrix example:

[[1 0 0 0 0] [6 4 0 0 0] [4 2 9 0 0] [1 1 1 1 0] [2 2 2 2 2]]

def PLU(A) ok1 small le-12 nscipy.shape (A) [0] Ucopy.copy(A) Lscipy.identity(n) P = scipy.identity(n) for j in range (1,n): # set to if we encoun # pivots smaller than t # initialize L, U and p # loop over columns -1 s scipy.argma x ( abs(ulj-1:n, j-1])) if s !- j-1: + j # find the largest num # if the largest number Uswap(U,s,j-1,n) if j>l: Lswap (L,s,j-1,j-1) for i in range(j+1,n+l): # check for zero pivot if abs (U[j-1,j-1])small: print( "Near-zero pivot!") ok reak for k in range (j,ntl): return L,U,P,ok def swap (M,i,j,k) # swap rows i and j from column up to (not including) k dum = copy . copy (M[i,0:k]) M[i,0:k]-copy.copy (M[j,0:k]) M[j,0:k]-copy.copy(dum) return M def PLU(A) ok1 small le-12 nscipy.shape (A) [0] Ucopy.copy(A) Lscipy.identity(n) P = scipy.identity(n) for j in range (1,n): # set to if we encoun # pivots smaller than t # initialize L, U and p # loop over columns -1 s scipy.argma x ( abs(ulj-1:n, j-1])) if s !- j-1: + j # find the largest num # if the largest number Uswap(U,s,j-1,n) if j>l: Lswap (L,s,j-1,j-1) for i in range(j+1,n+l): # check for zero pivot if abs (U[j-1,j-1])small: print( "Near-zero pivot!") ok reak for k in range (j,ntl): return L,U,P,ok def swap (M,i,j,k) # swap rows i and j from column up to (not including) k dum = copy . copy (M[i,0:k]) M[i,0:k]-copy.copy (M[j,0:k]) M[j,0:k]-copy.copy(dum) return M