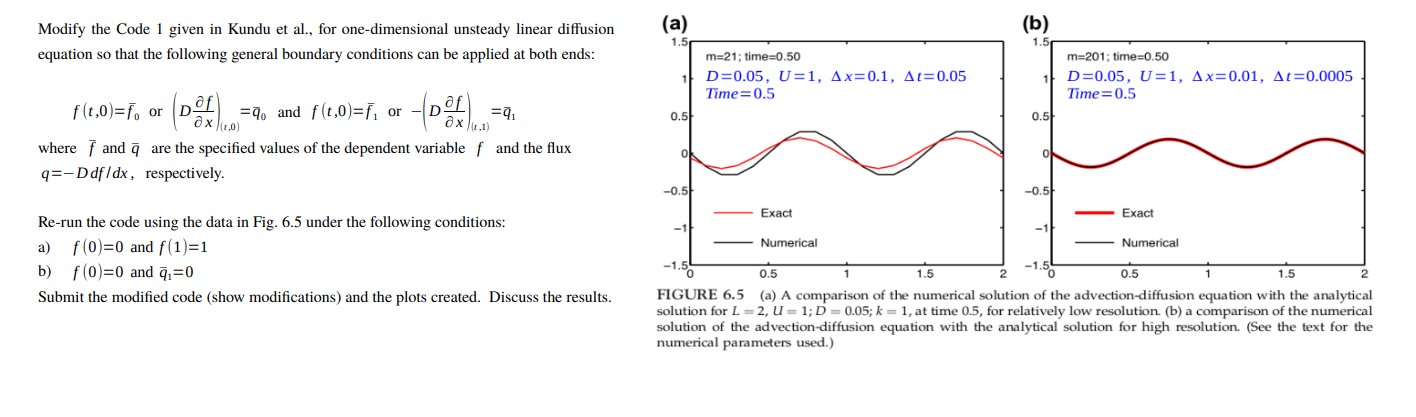
Modify the Code 1 given in Kundu et al., for one-dimensional unsteady linear diffusion equation so that the following general boundary conditions can be applied at both ends: (a) 1.5 m=21; time=0.50 1 f(t,0)= or D af =40 and f (t,0)=1, or - (Dof()) =91 (1.1) 0.5 where and are the specified values of the dependent variable f and the flux q=-Ddf/dx, respectively. 0 Re-run the code using the data in Fig. 6.5 under the following conditions: a) f(0)=0 and f(1)=1 D=0.05, U=1, Ax=0.1, At=0.05 Time=0.5 -0.5 Exact -1 Numerical -1.5 0.5 (b) 1.5 0.5 0 m=201; time=0.50 D=0.05, U=1, Ax=0.01, At=0.0005 Time=0.5 -0.5- Exact -1 Numerical 2 -1.5 0.5 b) f(0)=0 and q=0 Submit the modified code (show modifications) and the plots created. Discuss the results. 1.5 1 1.5 2 FIGURE 6.5 (a) A comparison of the numerical solution of the advection-diffusion equation with the analytical solution for L = 2, U=1; D = 0.05; k = 1, at time 0.5, for relatively low resolution. (b) a comparison of the numerical solution of the advection-diffusion equation with the analytical solution for high resolution. (See the text for the numerical parameters used.)