1. Modify the Gauss-Seidel function you completed in Lab 6, such that the function checks if the diagonal entries are zero. If needed, the function will swap the row that has a zero diagonal element with the next suitable row in A such that a matrix with non-zero diagonal elements is obtained. The function needs to record the swapping process by creating a permutation matrix, P. Use this function to solve the system. Set the tolerance for relative norm of residuals to 0.01, and report the number of iterations needed to reach this accuracy.

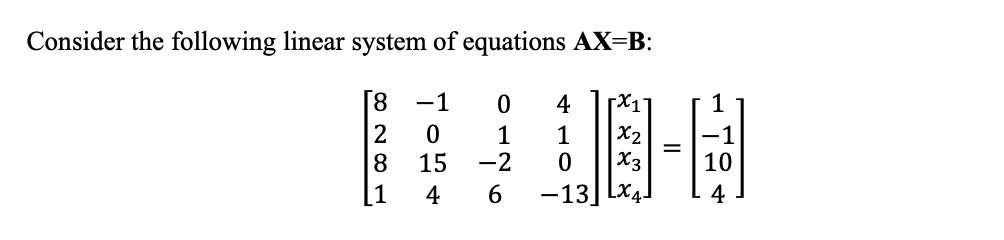
Consider the following linear system of equations AX=B: 8 2 8 1 -1 0 15 4 0 1 -2 6 4 X1 1 X2 0 -13 Lx 10 4 = == n function [x_Gauss,X, error_metric, relative_residual_error, kk] GaussMethod(A,b,x0, imax, tol); x = nan(imax, length(b)); % Iteration k = 1 x(1,:) = x0; n = length(b); for kk = 2:imax for ii = 1:n if ii == 1 x(kk, ii) (1/A(ii,ii))*(b(ii) sum(A(ii,ii+1:n).*x(kk-1,2:end))); elseif ii x(kk, ii) = (1/A(ii,ii))*(b(ii) sum(A(ii,1:n-1).**(kk, 1:n-1))); else x(kk, ii) (1/A(ii,ii))*(b(ii) sum(A(ii,1:ii-1).*x(kk, 1:ii-1)) - sum(A(ii,ii+1:n).**(kk-1, ii+1:n))); end end error_metric(kk-1) norm(x(kk, :) x(kk-1,:)); relative residual_error(kk) = norm(A*x(kk, :).' -b)orm(b); if error_metric(kk-1)