Module 3: Integer LP & Special Cases (QUESTION 1)

** I ALREADY HAVE PART A ANSWERED. PLEASE DISREGARD THE GREY BOX COVERING AN ANSWER CHOICE**

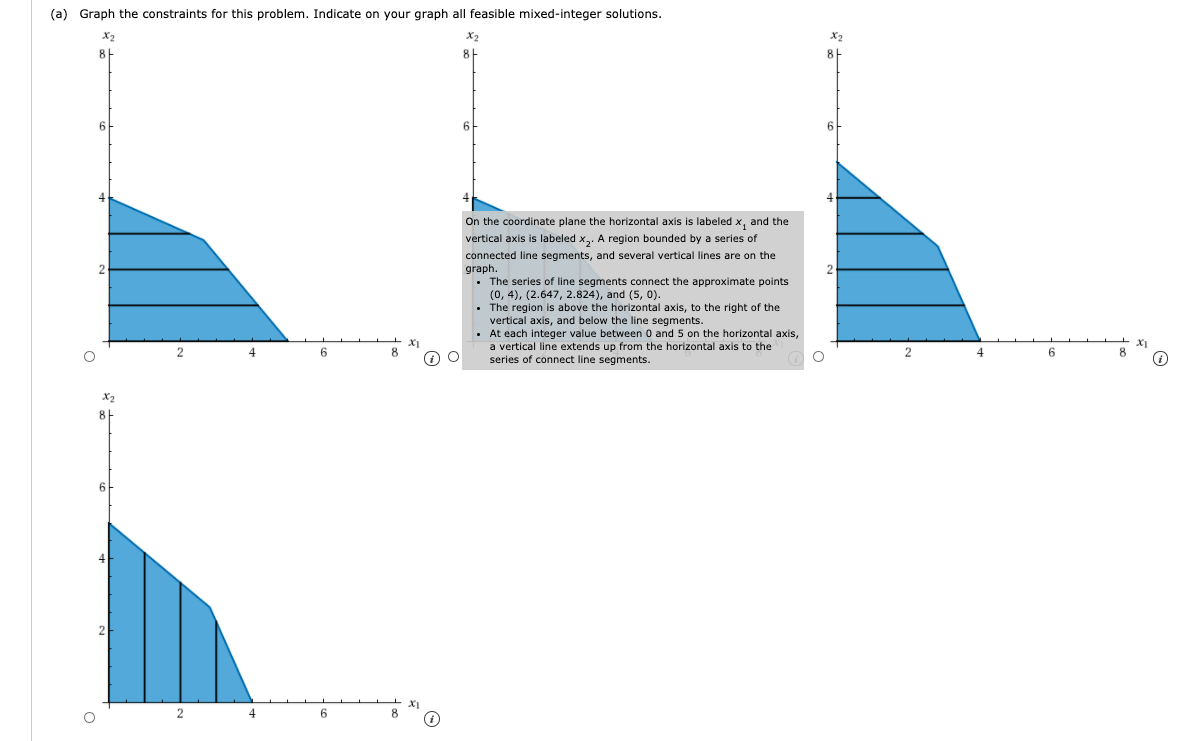
1. DETAILS ASWMSCI15 7.E.005. Consider the following mixed-integer linear program. Max 3x1 + 4x2 s.t. 4X1 + 9x2 = 36 6X1 + 5x2 = 30 *1,*2 2 and d x1 integer (a) Graph the constraints for this problem. Indicate on your graph all feasible mixed-integer solutions. X2 X2 X2 8 6 6 4 On the coordinate plane the horizontal axis is labeled x, and the vertical axis is labeled xz. A region bounded by a series of connected line segments, and several vertical lines are on the graph. The series of line segments connect the approximate points (0,4), (2.647, 2.824), and (5,0). The region is above the horizontal axis, to the right of the vertical axis, and below the line segments. At each integer value between 0 and 5 on the horizontal axis, a vertical line extends up from the horizontal axis to the series of connect line segments. X 4 6 4 O 6 8 X2 8 2 X1 2 4 6 8 (b) Find the optimal solution to the LP Relaxation. Round the value of xdown to find a feasible mixed-integer solution. (Round the values of X, and the optimal solution to three decimal places, if necessary.) at (x,y X3) =([ Is this solution optimal? O Yes O No (c) Find the optimal solution for the mixed-integer linear program. (Round your answers to three decimal places, when necessary.) at (x1, x2) =