Module 3: Integer LP & Special Cases (QUESTION 4)

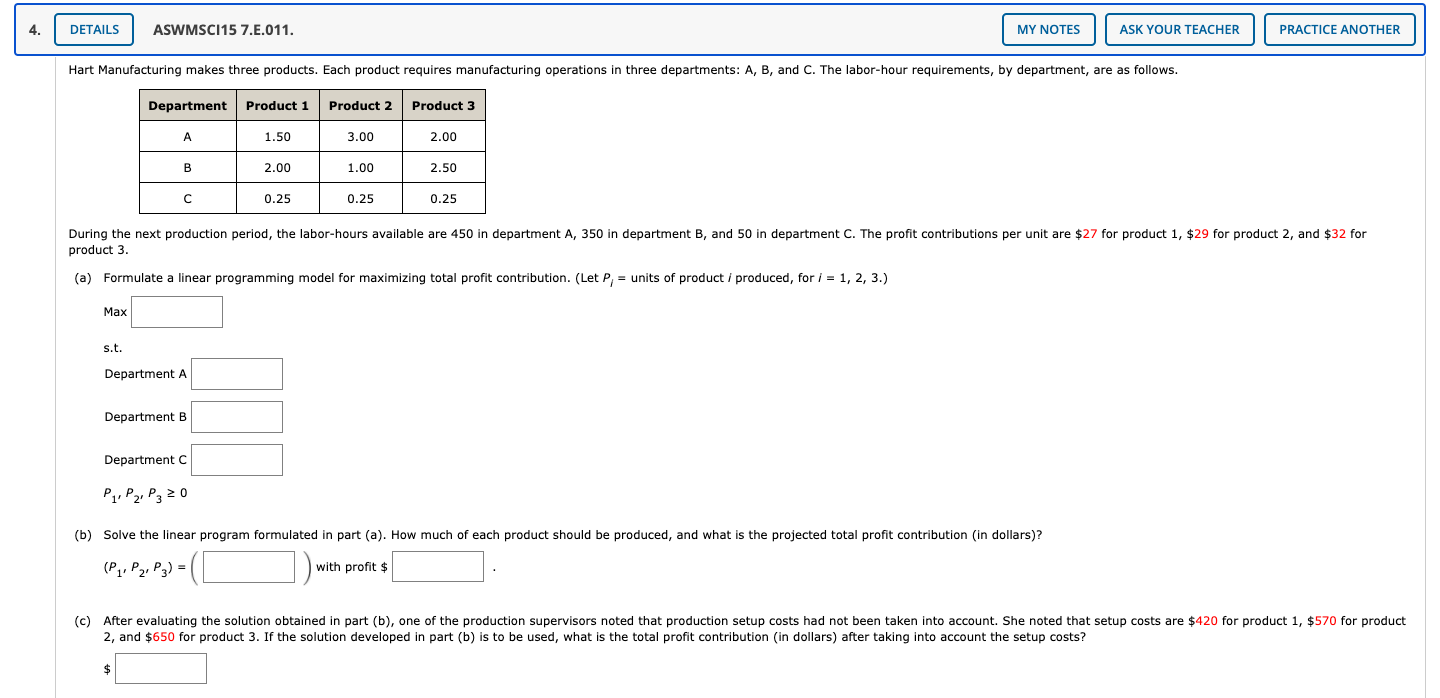
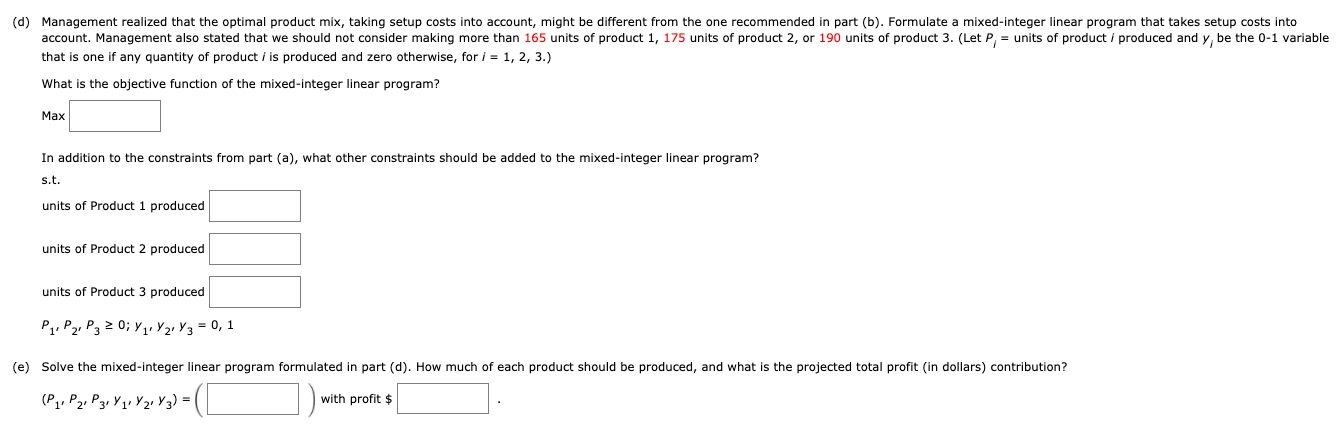
4. DETAILS ASWMSCI15 7.E.011. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows. Department Product 1 Product 2 Product 3 A 1.50 3.00 2.00 B 2.00 1.00 2.50 0.25 0.25 0.25 During the next production period, the labor-hours available are 450 in department A, 350 in department B, and 50 in department C. The profit contributions per unit are $27 for product 1, $29 for product 2, and $32 for product 3. (a) Formulate a linear programming model for maximizing total profit contribution. (Let P, = units of product i produced, for i = 1, 2, 3.) Max s.t. Department A Department B Department C Pa, P2, P 20 (b) Solve the linear program formulated in part (a). How much of each product should be produced, and what is the projected total profit contribution (in dollars)? (P1 P2, P3) = ]) with profit $ (c) After evaluating the solution obtained in part (b), one of the production supervisors noted that production setup costs had not been taken into account. She noted that setup costs are $420 for product 1, $570 for product 2, and $650 for product 3. If the solution developed in part (b) is to be used, what is the total profit contribution (in dollars) after taking into account the setup costs? $ (d) Management realized that the optimal product mix, taking setup costs into account, might be different from the one recommended in part (b). Formulate a mixed-integer linear program that takes setup costs into account. Management also stated that we should not consider making more than 165 units of product 1, 175 units of product 2, or 190 units of product 3. (Let P, = units of product i produced and y, be the 0-1 variable that is one if any quantity of product i is produced and zero otherwise, for i = 1, 2, 3.) What is the objective function of the mixed-integer linear program? Max In addition to the constraints from part (a), what other constraints should be added to the mixed-integer linear program? s.t. units of Product 1 produced units of Product 2 produced units of Product 3 produced P1 P2, P3 2 0; Y 14Y2: V3 = 0,1 (e) Solve the mixed-integer linear program formulated in part (d). How much of each product should be produced, and what is the projected total profit in dollars) contribution? (P2, P2, P3, Y 14Y2:43) with profit $