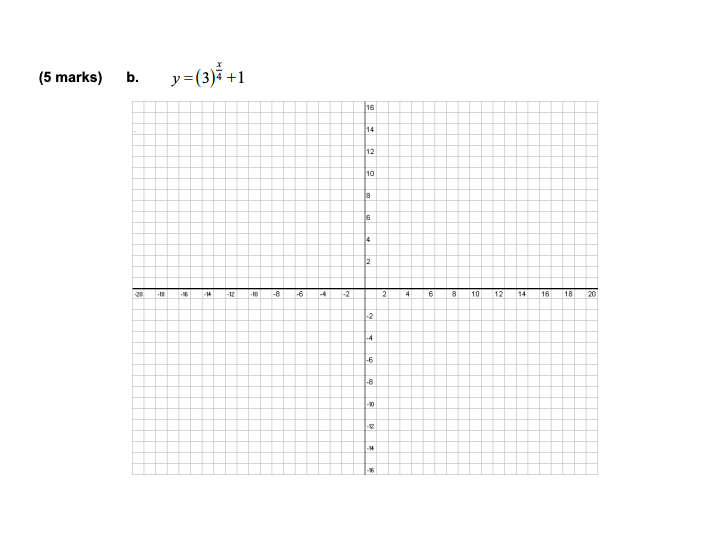
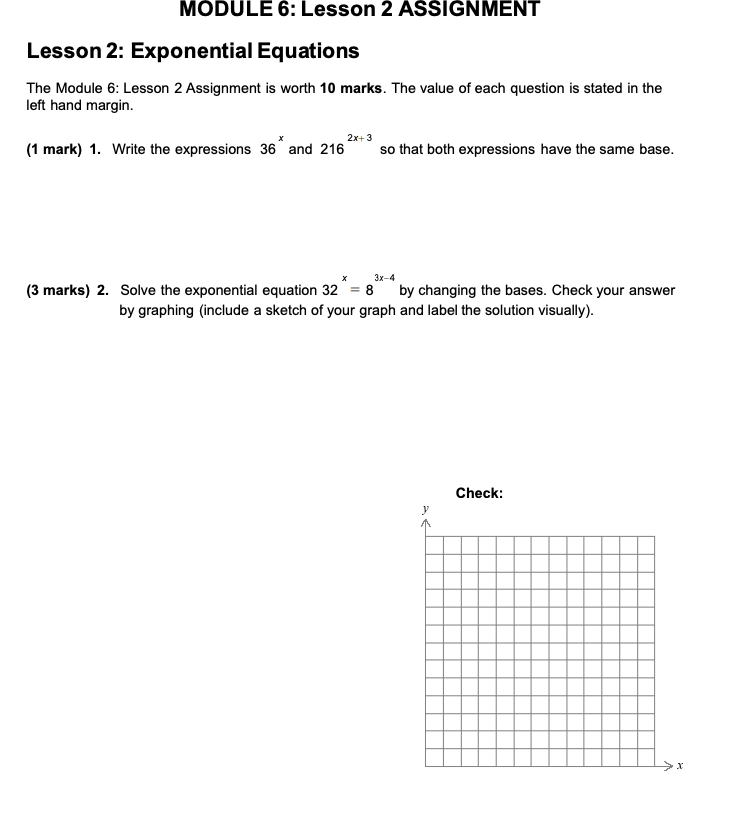
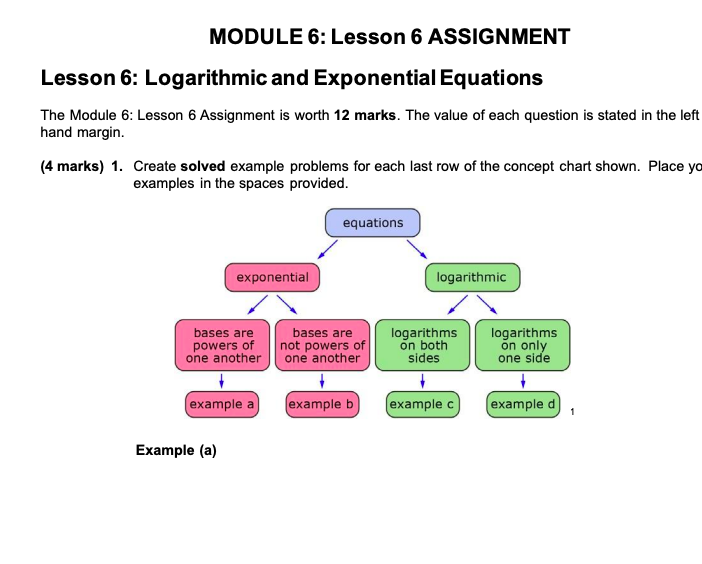
MODULE 6: Lesson 1 ASSIGNMENT Lesson 1: Exponential Functions The Module 5: Lesson 1 Assignment is Wr'th 13 marks. The value of each question is stated in the left hand margin. 1. Complete these tasks for each of the following functions. I. Describe the transformations of the function x} = swim\"4' + it that occurred. ll. Sketch the graph of the function. ill. Identify the domain, range, equation of the horizontal asymptote, and intercepts. _is :H- :Io \f2. The radioactive isotope molybdenum-99 is produced at Chalk River Laboratories. Molybdenum-99 has a half-life of 66 h. (1 marks) a. What is the exponential function that would describe the relationship between the percent, P of molybdenum-99 remaining after t hours? (2 marks) b. What percent of molybdenum-99 would be left after 24 h?MODULE 6: Lesson 2 ASSIGNMENT Lesson 2: Exponential Equations The Module 5: Lesson 2 Assignment is worth 1D marks. The 1value of each question is stated in the left hand margin. 1 213 (1 mark} 1. 1Ii'il'rite the expressions 36 and 215 so that both expressions have the same base. x 314 (3 marks} 2. Solve the exponential equation 32 = B by changing the bases. Check your answer by graphing {include a sketch of your graph and label the solution visually}. Mathematics 30-1 2 Assignment Booklet 6 - *+4 _2x (3 marks) 3. Solve the exponential equation 25 = 625 by changing the bases. Check your answer using substitution. Check: LS RS (3 marks) 4. Trinh has decided to save money to buy a new computer. She invests $800 in an account that earns 5.0% per year, compounded quarterly. Determine how long she needs to invest her money until she has $1000. Completely explain the process you used to solve this problem - use the pages provided. NOTE: You may not use logarithms to solve this problem.MODULE 6: Lesson 3 ASSIGNMENT Lesson 3: Understanding Logarithms The Module 6: Lesson 3 Assignment is worth 16 marks. The value of each question is stated in the left hand margin. (1 mark) 1. Rewrite the logarithmic equation into exponential form with a positive exponent. logR M | = -H 2. Evaluate each logarithm using the exponential method. (1 mark) a. log, 1024 (1 mark) b. log2 00 1 - (1 mark) c. log, (V/27)Mathematics 301 2 Assignment Booklet E 3. Determine the value of a in each of the following equations using the method shown in the lesson. [2 marks} a. log}; a = 3 2 (2 marks} b. log 16 = E [3 marks} 4. A possible logarithmic function that ooulo model the growth of a tree is h = allog3 t where h is the height of the tree in metres and t is the time in years. Estimate the approximate height of the tree to the nearest tenth of a metres after 1i] year's. Explain the reasoning for your estimation. Mathematics 301 3 Assignment Booklet (3 marks} 5. The formula for the Richter magnitude, M, of an earthquake is M = lggi r where A is An the amplitude of the earthquake and A0 is the amplitude of a standard earthquake with magnitude of t]. In 2D11, an earthquake occurred off the Pacic coast of the Tohoku region of Japan. This earthquake, which measured 9.0 on the Richter scale, is one of the ve most powerful earthquakes in the world since modern record-keeping began in t'EItZItZI. By comparison, one of the largest earthquakes to hit Alberta was a magnitude 4.? earthquake. This earthquake occurred in 1934, on the border between British Columbia and Alberta, just north of Waterton Lakes National Park. Determine how many.f times larger in amplitude the Tohoku earthquake was compared to the Alberta quake. Express your answer to the nearest ten thousand. (2 marks} 5. If a third earthquake is 3GB times larger in amplitude than the Alberta quake, then what is the magnitude of the third earthquake? Mathematics 301 1 Assignment Booklet IE MODULE 6: Lesson 4 ASSIGNMENT Lesson 4: Graphing Logarithmic Functions The Module 5: Lesson 4 Assignment is worth 1!!! marks. The 1uralue of each question is stated in the left hand margin. 1. Consider the functions fix} log2 x and g [xi 2log2 tx 314. [2 marks] a. Find the domain and range for each function. (2 marks] b. Explain how the graph gm can be described as a transformation of fix]. (3 marks] 2. The graph of x} log:i x is - vertically stretched about the x-ar-ris by a factor of E I horizontally stretched about the yaxis by a factor of 3 I translated 5 units to the right and 2 units down If the equation of the transformed image is 1rrrritten in the form gfx} = a logbfx c}] + of determine the values of e, b, c, and d. Then write the equation of gut}. Mathematics 30-1 2 Assignment Booklet 6 3. The slope of a beach is influenced by the local tides, wind and wave patterns, and the size of the sand particles on the beach. In general, as the diameter in millimetres, d, of the average size of the particles on the beach increases, the slope of the beach, s, increases according to the formula s(d) = 0.159 + 0.1181 log d. (1 mark) a. Describe the graph of the function s(d) as compared to the graph of f (d) = log d using transformations terminology. (2 marks) b. If the slope of a particular beach is 0.005 (about a 1-m vertical climb for every 200 m in the horizontal direction), algebraically determine the average diameter (in millimetres) of a grain of sand on the beach. Round your answer to 4 decimal places.Mathematics 30-1 Assignment Booklet 6 MODULE 6: Lesson 5 ASSIGNMENT Lesson 5: Laws of Logarithms The Module 6: Lesson 5 Assignment is worth 25 marks. The value of each question is stated in the left hand margin. 1. Use the laws of logarithms to evaluate each expression. (1 mark) a. log10 106 - log10 109 (2 marks) b. 3log 2 6 -3log2 3 (3 marks) c. -log3 9-1093 12 + 21093 6Mathematics 30-1 2 Assignment Booklet 6 2. Expand each of the following expressions: (1 mark) a. log, (2x) (1 mark) b. logg (x3) 8x* (2 marks) c. log2 5 3. Write each expression as a single logarithm in simplest form. State any restrictions on the variable. (3 marks) a. log2 (x2 -16)-log, (2x -8)\fMathematics 30-1 Assignment Booklet 6 The pH scale is used to measure the acidity or alkalinity of a solution. The pH of a solution is defined as ph = -log [H*], where [H'] is the hydrogen ion concentration in moles per litre (mol/L). Solutions with a pH of less than 7 are acidic, and solutions with a pH of greater than 7 are basic, or alkaline. The lower the pH, the more acidic the solution. Battery Acid Increasing Acidity Lemon Juice -Vinegar UAWN 6 -Milk Neutral Baking Soda 10 Increasing 11 Milk of Magnesia Alkalinity 12 Ammonia 13 Lye 14 (3 marks) a. A common ingredient in cola drinks is phosphoric acid, the same ingredient found in many rust removers. A cola drink has a pH of 2.5. Milk has a pH of 6.6. How many times as acidic as milk is a cola drink?Mathematics 30-1 5 Assignment Booklet 6 (3 marks) b. An apple is 5 times as acidic as a pear. If a pear has a pH of 3.8, what is the pH of an apple?MODULE 6: Lesson 6 ASSIGNMENT Lesson 6: Logarithmic and Exponential Equations The Module 6: Lesson 6 Assignment is worth 12 marks. The value of each question is stated in the left hand margin. (4 marks) 1. Create solved example problems for each last row of the concept chart shown. Place yo examples in the spaces provided. equations exponential logarithmic bases are bases are logarithms logarithms powers of not powers of on both on only one another one another sides one side example a example b example c example d 1 Example (a)\f\f\fMathematics 30-1 6 Assignment Booklet 6 (2 marks) 2. a. You have $5000 to invest into a TFSA (Tax Free Savings Account). Suppose your financial advisor proposes two different accounts for you to invest in. i) 7% interest compounded quarterly ii) 7% interest compounded semi-annually If your goal is to have your investment double in value, which account should you choose and why? (3 marks) b. How long will it take to double the investment with each account?Mathematics 301 ? Assignment Booklet (3 marks} 4. There is a relationship between mortgage amount, number of payments, amount of each payment, how often each payment is made, and the interest rate. The following formula illustrates the relationship: PF 2 R[1{1_+r}'\"] l! t Ft:r = present value o l : interest rate per compounding period, as a decimal Ir Ft = payment amount Ir n = number of payments Suppose a bank offers you a 3.4% interest rater compounded semi-annually, on a mortgage amount of $1?3 112. You pay $1lmo, or How semi-annually. How many semi-annual payments would you have to make to pay off the mortgage? How long, in years, would it take to pay off the mortgage