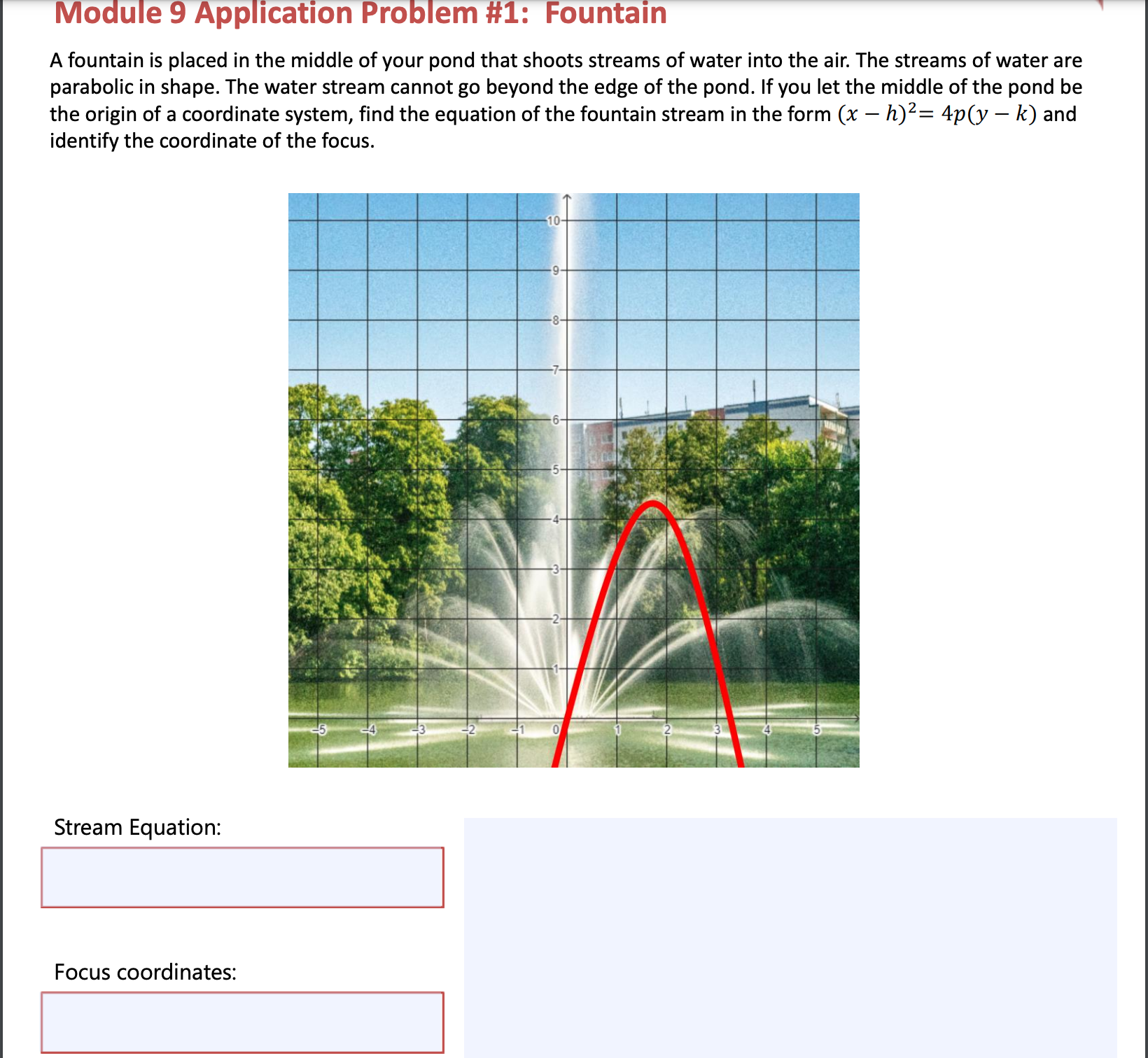
Module 8 Application Problem #1: Garden Shed Paint A garden shed is needed to be placed near your garden to house all the tools and necessities to maintain the garden. Design a garden shed for your park. Be sure to include specifics including the shape, the dimensions, and the pitch (slope) of the roof. Then calculate the area of the sides of the garden shed to determine how much paint would be needed to cover it. The paint chosen to paint your garden shed costs $34.95 per gallon. How much will it cost to paint your shed? Assume that you cannot buy partial gallons. Shape: Dimensions: Pitch (slope): Area of sides: I Module 8 Application Problem #2: Garden Shed Shingles ' Calculate the surface area of the roof. A bundle of roof shingles covers about 33 ft>. How many bundles will you need for your garden shed? Assume you cannot buy partial bundles. Surface Area: I Number of bundles: I Module 9 Application Problem #1: Fountain A fountain is placed in the middle of your pond that shoots streams of water into the air. The streams of water are parabolic in shape. The water stream cannot go beyond the edge of the pond. If you let the middle of the pond be the origin of a coordinate system, find the equation of the fountain stream in the form (x h)?= 4p(y k) and identify the coordinate of the focus. L e ] i Stream Equation: Focus coordinates: . Module 9 Application Problem #2: Swing Sets Swing sets are added to the playground. When children are swinging on them, the largest safe angle to swing through from the perpendicular is 55 degrees, making a 110 degree total pendulum swing. What is the arc length of this swing? Note: this will require you to decide how long the rope of the swing is first. It is encouraged to do a little research to see what reasonable swing lengths include. You are trying to decide how far away an additional play structure can be placed to not get in the way of the swing. When a child is at the peak of their swing, what is the horizontal distance between them and the perpendicular? Research to decide this length. Swing length: Arc length: Modules 8-9 Application Problems Reflection Prompt: Connect What experience, creation, or idea did you explore with your garden shed? From what unique perspective did you explore the fountain and swing sets? How did these ideas connect to ideas or concepts from diverse areas of interests