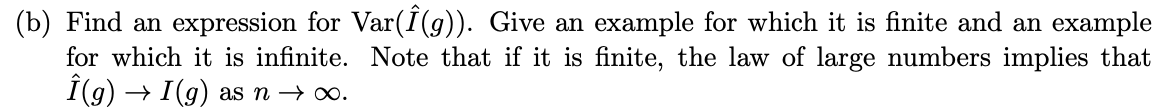
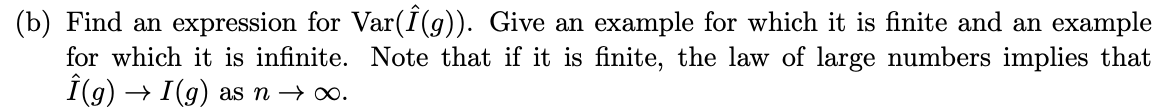
Monte Carlo integration is a method to numerically estimate integral like I(9) = Jog(x)dx. The idea is to sample X1, X2, ..., Xn independent Unif(a, b) and estimate I(9) as , Et-19(Xi). This problem introduces a variation on the Monte Carlo integration technique. Let h(x) be a density function on [a, b]. Generate X1, ..., Xn independently from h(x) and estimate I(g) by i(g) = 1Eng(X;) 1 h ( Xi ) (a) Show that E[I(9)] = I(9).(b) Find an expression for Var(I(g)). Give an example for which it is finite and an example for which it is infinite. Note that if it is finite, the law of large numbers implies that 1(g) - I(g) as n + 00