Monte Carlo Simulation

This lab assignment consists of two problems involving Monte Carlo simulation. You should use Python for this assignment. Develop a Python script (program) for each problem and please make sure that the code is fully commented. In addition to the code, submit a Word document file containing the write-up answering the questions for each case. Zip together the three files and submit on canvas.

References: Seila, A. F., V. Ceric, and P. Tadikamalla, Applied Simulation Modeling, Duxbury - Brooks/Cole, Belmont, CA, 2003. Schriber, T. J., Simulation for the Masses: Spreadsheet-based Monte Carlo Simulation, Proceedings of the 2009 Winter Simulation Conference, Rossetti, Hill, Johansson, Dunkin, and Ingalls, Eds., December 2009.

1. Adopted from Problem 2.13 from Seila et al. (page 74) with minor changes The actuaries for an insurance company represent the total losses experienced during a week as follows: Let N represent the number of policies that experience a loss during the week, and Z1, Z2, be independent random variables that have the same distribution representing the amount of each loss. Then the total losses for the week are X = Z1 + Z2 + Z3 + + ZN Using probability theory, one can show that if N and Z1, Z2, are statistically independent, the expected value of X is E(X) = E(N)*E(Z) Thus, under these assumptions, it is easy to compute the mean loss during a week; however, it is not so easy to establish the probability distribution of the total loss.

a) Let N have a discrete uniform distribution over the values 50 to 145 and let each Zi have a symmetric triangular distribution between $280 and $740. Develop a Monte Carlo simulation to estimate the total weekly loss and run the simulation for 5000 independent replications.

b) Using the data from the simulation, compute the sample mean, sample standard deviation, the 95% confidence interval on the mean and the 25th and 75th percentiles of the sample. Compare the confidence interval of the mean to the value computed from the expression for E(X).

c) Estimate the probability that the loss will be less than $40,000 and the probability that the loss will be greater than $70,000. INSY 3420

2.)

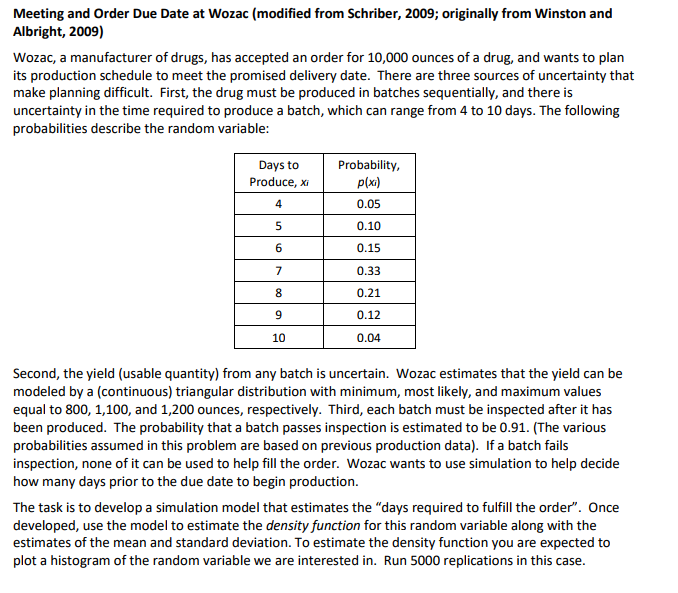
Meeting and Order Due Date at Wozac (modified from Schriber, 2009; originally from Winston and Albright, 2009) Wozac, a manufacturer of drugs, has accepted an order for 10,000 ounces of a drug, and wants to plan its production schedule to meet the promised delivery date. There are three sources of uncertainty that make planning difficult. First, the drug must be produced in batches sequentially, and there is uncertainty in the time required to produce a batch, which can range from 4 to 10 days. The following probabilities describe the random variable Probability p(xi) 0.05 0.10 0.15 0.33 0.21 0.12 0.04 Days to Produce, Xi 4 10 Second, the yield (usable quantity) from any batch is uncertain. Wozac estimates that the yield can be modeled by a (continuous) triangular distribution with minimum, most likely, and maximum values equal to 800, 1,100, and 1,200 ounces, respectively. Third, each batch must be inspected after it has been produced. The probability that a batch passes inspection is estimated to be 0.91. The various probabilities assumed in this problem are based on previous production data). If a batch fails inspection, none of it can be used to help fill the order. Wozac wants to use simulation to help decide how many days prior to the due date to begin production. The task is to develop a simulation model that estimates the "days required to fulfill the order". Once developed, use the model to estimate the density function for this random variable along with the estimates of the mean and standard deviation. To estimate the density function you are expected to plot a histogram of the random variable we are interested in. Run 5000 replications in this case Meeting and Order Due Date at Wozac (modified from Schriber, 2009; originally from Winston and Albright, 2009) Wozac, a manufacturer of drugs, has accepted an order for 10,000 ounces of a drug, and wants to plan its production schedule to meet the promised delivery date. There are three sources of uncertainty that make planning difficult. First, the drug must be produced in batches sequentially, and there is uncertainty in the time required to produce a batch, which can range from 4 to 10 days. The following probabilities describe the random variable Probability p(xi) 0.05 0.10 0.15 0.33 0.21 0.12 0.04 Days to Produce, Xi 4 10 Second, the yield (usable quantity) from any batch is uncertain. Wozac estimates that the yield can be modeled by a (continuous) triangular distribution with minimum, most likely, and maximum values equal to 800, 1,100, and 1,200 ounces, respectively. Third, each batch must be inspected after it has been produced. The probability that a batch passes inspection is estimated to be 0.91. The various probabilities assumed in this problem are based on previous production data). If a batch fails inspection, none of it can be used to help fill the order. Wozac wants to use simulation to help decide how many days prior to the due date to begin production. The task is to develop a simulation model that estimates the "days required to fulfill the order". Once developed, use the model to estimate the density function for this random variable along with the estimates of the mean and standard deviation. To estimate the density function you are expected to plot a histogram of the random variable we are interested in. Run 5000 replications in this case