Most structures designed for seismic forces lower than the ones needed for an elastic response during the design earthquake. However, design of structures in the elastic range for rare seismic events are considered uneconomical and we also witnessed in the past that structures designed for a small fraction of the forces necessary for an elastic response, survived major earthquakes though with moderate to heavy damages. The overall effect of inelastic response is increase in displacement and possible reduction in force. Don't forget that inelastic response of structures mean damage to some degree.

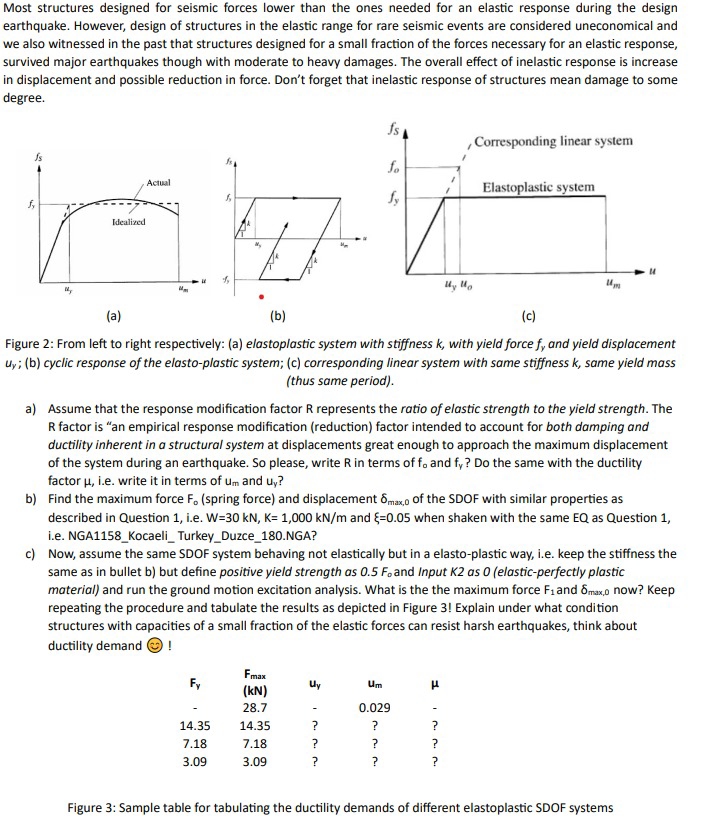
Figure $2$: From left to right respectively: $($a$)$ elastoplastic system with stiffness $k,$ with yield force $f_y$ and yield displacement $u_y$; $($b$)$ cyclic response of the elasto$-$plastic system; $($c$)$ corresponding linear system with same stiffness $k,$ same yield mass $($thus same period$).$

a$)$ Assume that the response modification factor R represents the ratio of elastic strength to the yield strength. The R factor is $"$an empirical response modification $($reduction$)$ factor intended to account for both damping and ductility inherent in a structural system at displacements great enough to approach the maximum displacement of the system during an earthquake. So please, write $R$ in terms of $f_o$ and $f_y?$ Do the same with the ductility factor $,$ i$.$e$.$ write it in terms of $u_m$ and $u_y?$

b$)$ Find the maximum force $F_o($spring force$)$ and displacement ${}_{\text{m}\text{a}\text{x}\text{,}0}$ of the SDOF with similar properties as described in Question $1,$ i$.$e$.W=30kN,K=1,000k\frac{N}{m}$ and $=0\mathrm{.}05$ when shaken with the same EQ as Question $1,$ i$.$e$.$ NGA$1158\_$Kocaeli$\_$Turkey$\_$Duzce$\_180.$NGA?

c$)$ Now, assume the same SDOF system behaving not elastically but in a elasto$-$plastic way, i$.$e$.$ keep the stiffness the same as in bullet b$)$ but define positive yield strength as $0\mathrm{.}5F_{\text{@}}$ and Input K$2$ as $0($elastic$-$perfectly plastic material$)$ and run the ground motion excitation analysis. What is the the maximum force $F_1$ and ${}_{\text{m}\text{a}\text{x}\text{,}}$ now? Keep repeating the procedure and tabulate the results as depicted in Figure $3!$ Explain under what condition structures with capacities of a small fraction of the elastic forces can resist harsh earthquakes, think about ductility demand $()!$

$\backslash$table$[[F_y,\backslash$table$[[F_{\text{m}\text{a}\text{x}}$