Multivariable Calculus Question

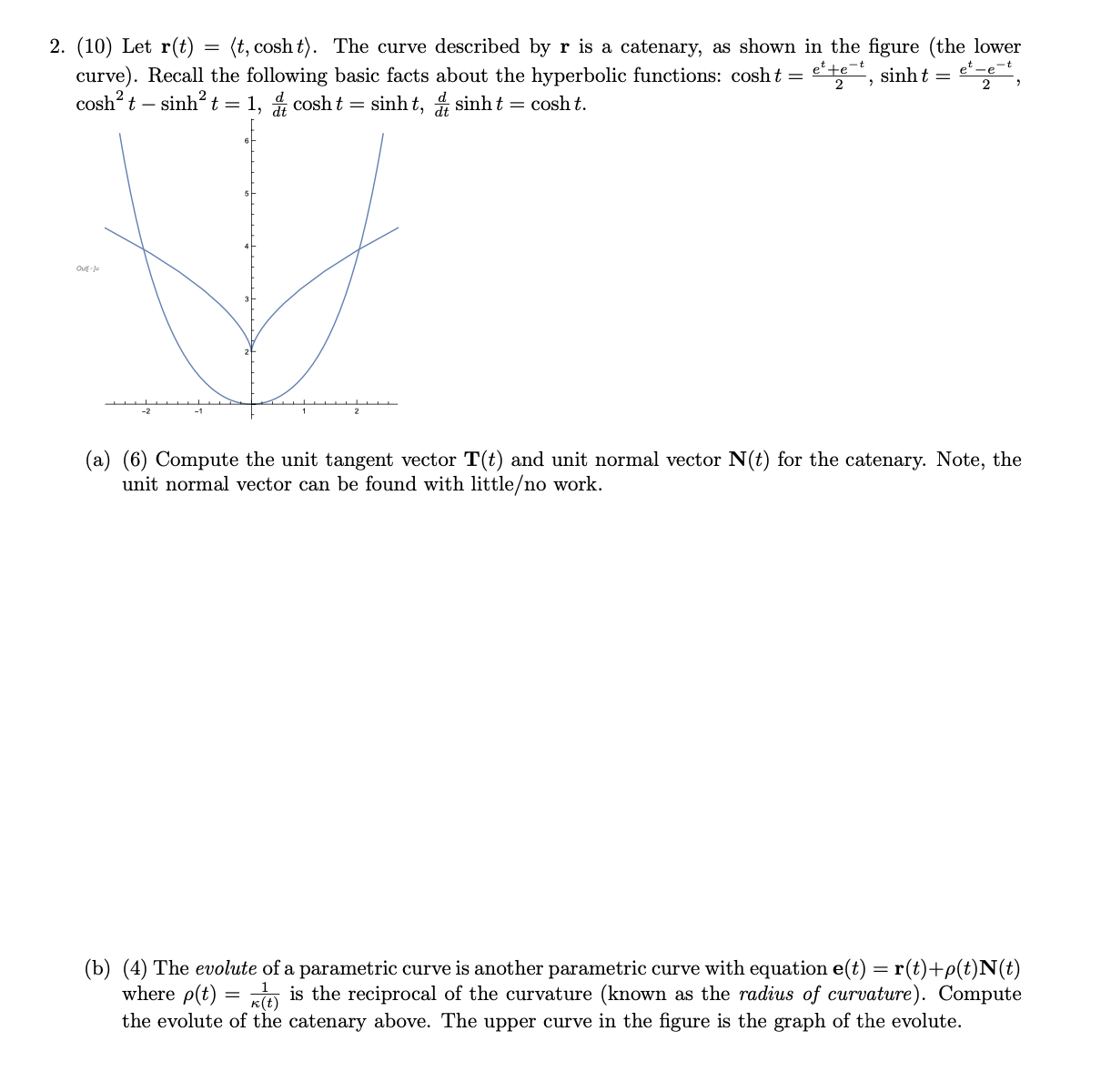
2. (10) Let r(t) = (t, cosht). The curve described by r is a catenary, as shown in the figure (the lower curve). Recall the following basic facts about the hyperbolic functions: cosht = ete 2 , sinht = erect cosh t - sinh t = 1, at cosh t = sinht, at sinht = cosh t. (a) (6) Compute the unit tangent vector T(t) and unit normal vector N(t) for the catenary. Note, the unit normal vector can be found with littleo work. (b) (4) The evolute of a parametric curve is another parametric curve with equation e(t) = r(t) +p(t) N(t) where p(t) = x() is the reciprocal of the curvature (known as the radius of curvature). Compute the evolute of the catenary above. The upper curve in the figure is the graph of the evolute