My code

% Creating a coefficient Matrix A

A = [1 3 -2 0 2 0; 2 6 -5 -2 4 -3; 0 0 0 1 5 3; 1 3 0 4 2 9;];

% Creating a column matrix b

b = [0; -1; 1; 3];

% Creating an Augmented Matrix

Ab = [A , b];

% Using rref to reduce

[rowreduceAb , pivotvarAb] = rref(Ab);

% Displaying the rowreducedAb and pivotvarAb

disp("Row reduced Matrix")

disp(rowreduceAb)

disp("Pivot Variable colums are")

disp(pivotvarAb)

% Getting the row and column of Augmented Matrix

[m , n] = size(Ab);

% If Rightmost column is pivot variable , we will show warning

if(n == max(pivotvarAb))

disp("Linear Equations has no solution.")

return;

end

% If Program does not terminate in previous line , then we will proceed

% ahead

% Getting the number of variable

[~ , numvars] = size(A);

% Displaying the number of variables

fprintf('Number of variables are %d ' , numvars);

% Getting the number of pivot variables

[~ , numpivotvars] = size(pivotvarAb);

% Displaying number of pivot variables

fprintf("Number of pivo variables are %d " , numpivotvars);

% Getting the number of free variables

numfreevars = numvars - numpivotvars;

% Displaying number of free variables

fprintf("Number of free variables are %d " , numfreevars);

%Store this number in numfreevars.

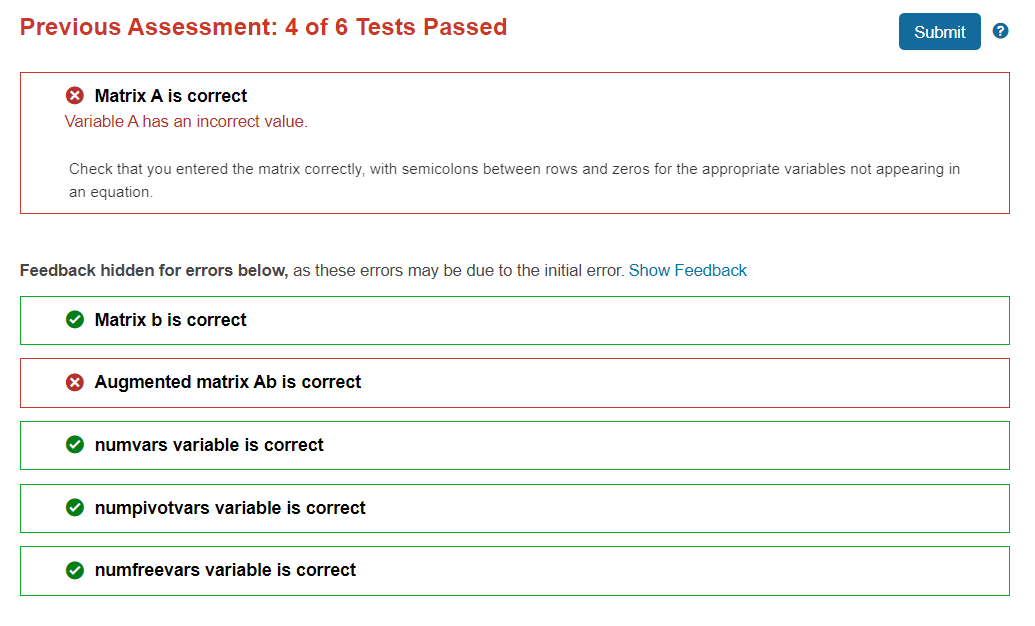
MATLAB: Augmented Matrices In this activity you will define an augmented matrix, find the number of pivot variables in the reduced system, and find the number of free variables in the solution to the linear system of equations. Consider the linear system of equations 2x + y = 3 x + 2y = 5 %Create the coefficient matrix C. C = [2 1; 1 2] Remember, to create a column matrix, the rows are separated %Create the column matrix d of constants. %by semicolons. d = [3; 5] %Create the augmented matrix [C] d. Store this augmented matrix in Cd. Cd - [CD] Store the reduced matrix in rowreducedCd, and %Use the rref) command to reduce the augmented matrix. %store pivot variables in pivotvarsCd [rowreducedcd, pivotvarsCd] = rref(Cd) %Warning: Look carefully at the reduced augmented matrix. If one of the pivot columns is the rightmost %column, the system of linear equation has no solution and no further analysis is possible. %Do you run into any difficulties? Explain what is happening as a comment in your code. Store this number %Use the size command to find the number of variables in the system of linear equations. %in numvars. [numeqns, numvars] = size(C) Store this number in numpivotvars. %Use the size command to find the number of pivot variables. [numrows, numpivotvars] = size(pivotvarsCd) %Use subtraction to find the number of free variables in the solution to the system of linear equations. %Store this number in numfreevars. numfreevars = numvars - numpivotvars Utilize the following linear system of equations for this activity. X] + 3x2 - 2x3 + 2x3 = 0 2x1 + 6x2 - 5x3 - 2x4 + 4x5 - 3x6 = -1 x3 + 5x4 + 3x6 = 1 x1 + 3x2 + 4x4 + 2x5 + 9x6 = 3 Previous Assessment: 4 of 6 Tests Passed Submit Matrix A is correct Variable A has an incorrect value. Check that you entered the matrix correctly, with semicolons between rows and zeros for the appropriate variables not appearing in an equation. Feedback hidden for errors below, as these errors may be due to the initial error. Show Feedback Matrix b is correct X Augmented matrix Ab is correct numvars variable is correct numpivotvars variable is correct numfreevars variable is correct