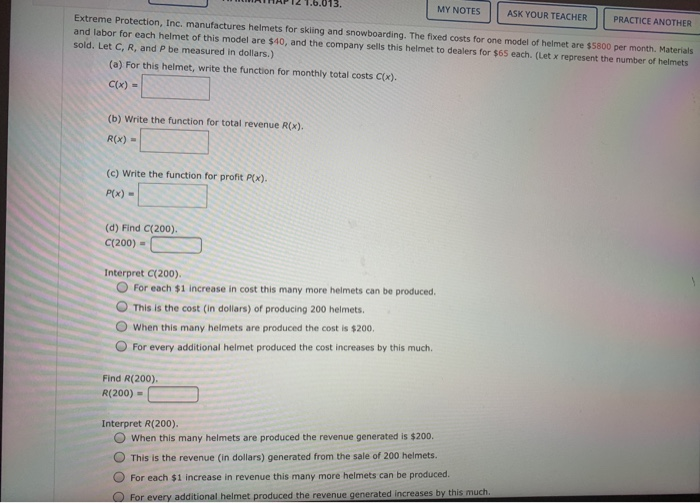
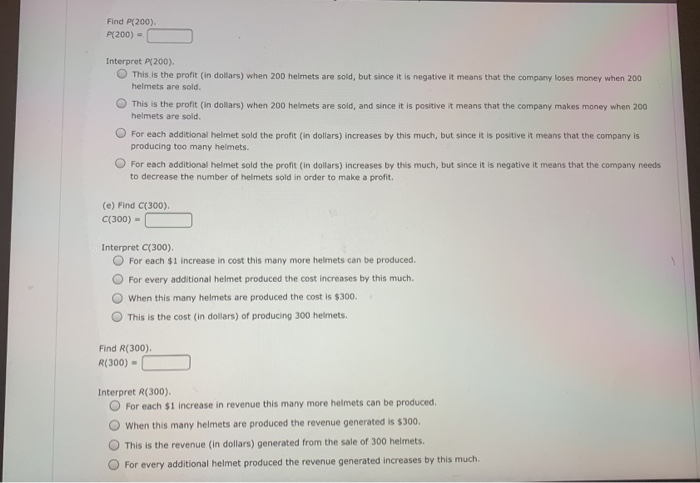
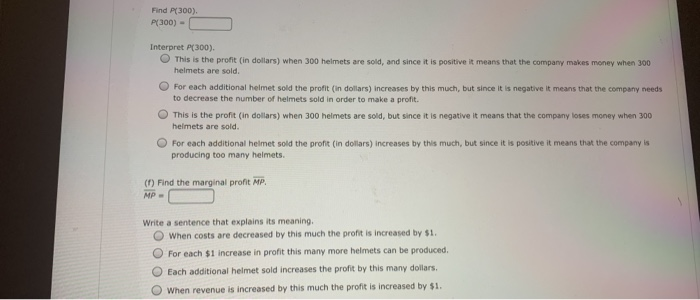
Question: MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Extreme Protection, Inc. manufactures helmets for skiing and snowboarding. The fixed costs for one model of helmet are
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


