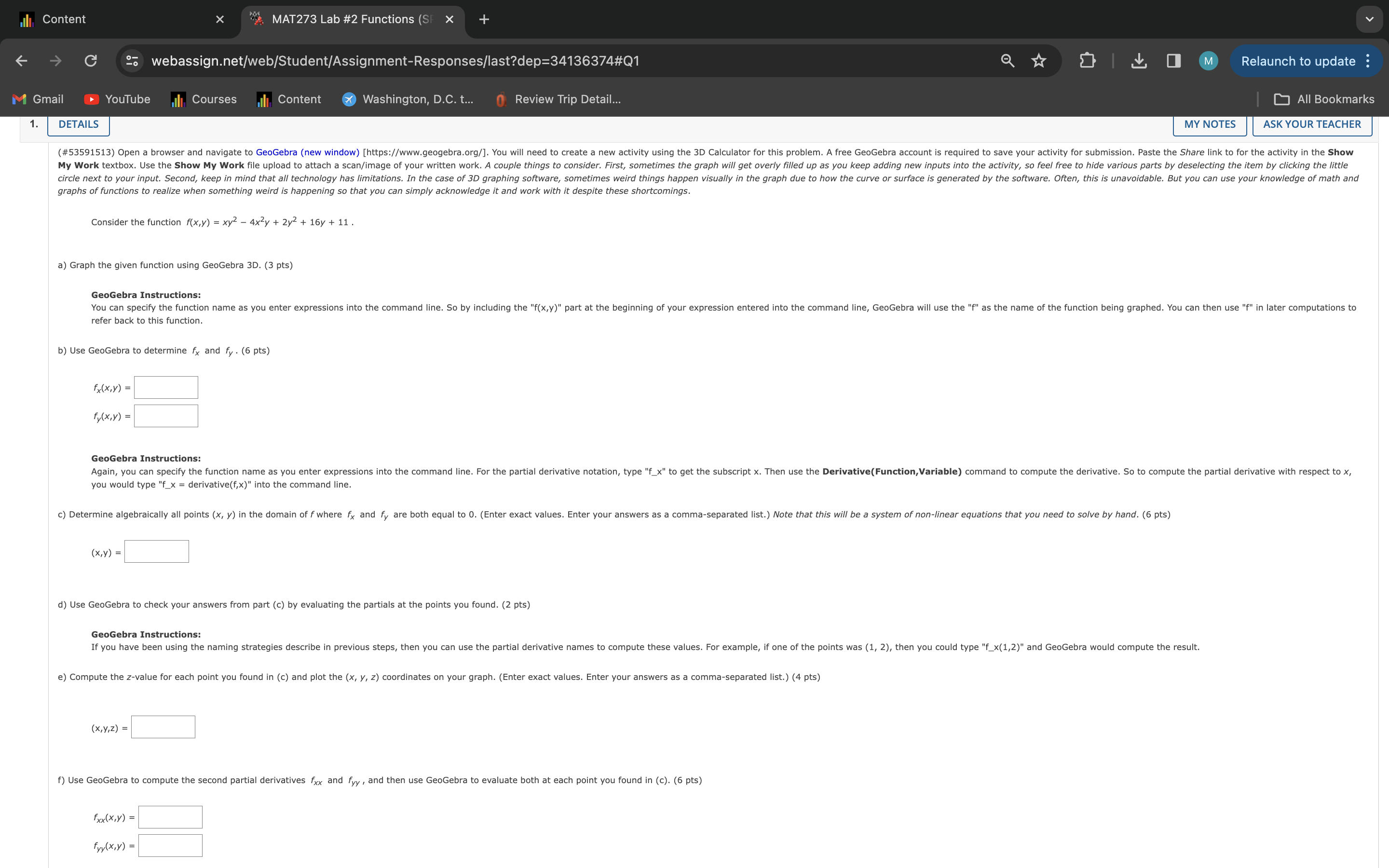
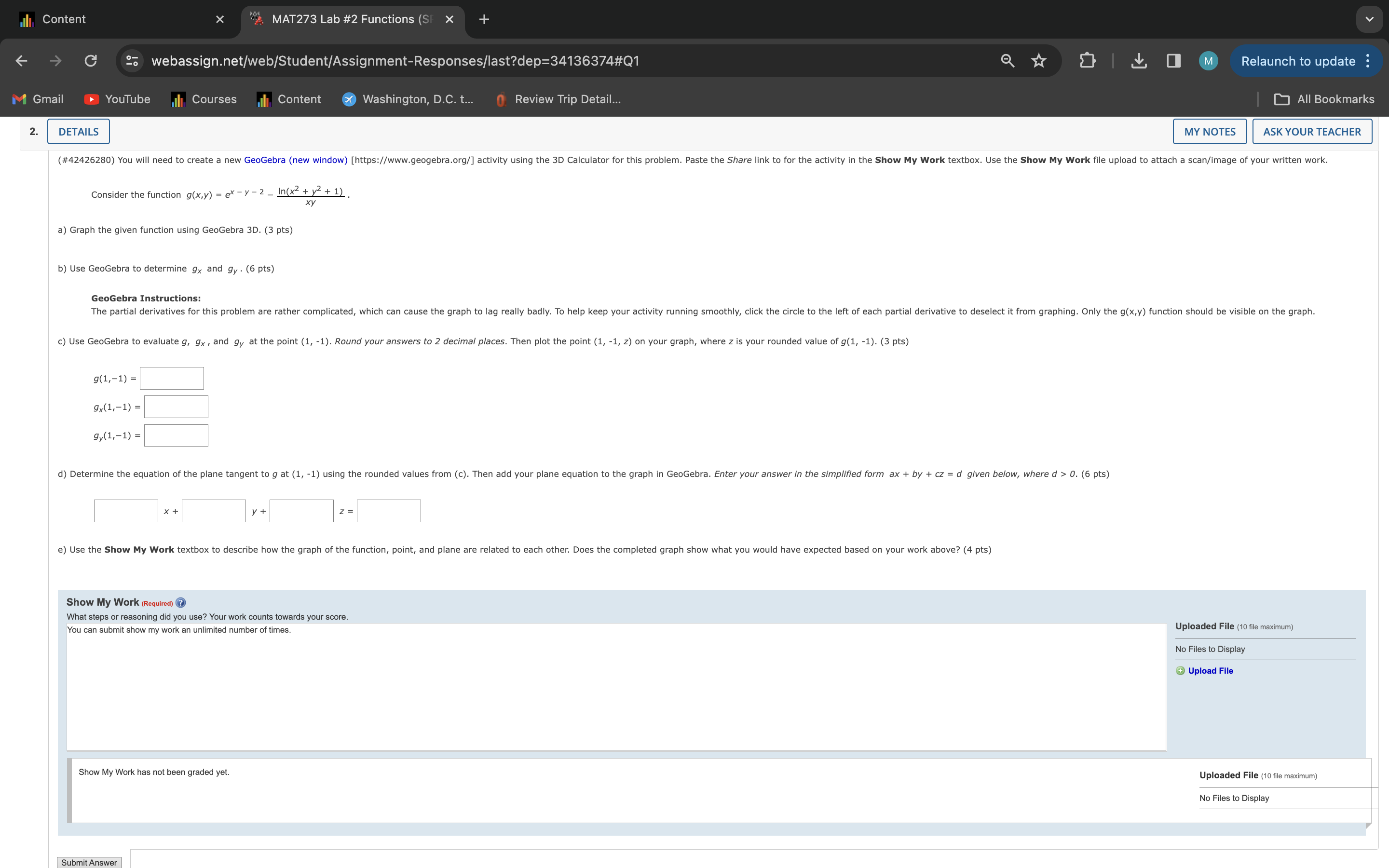
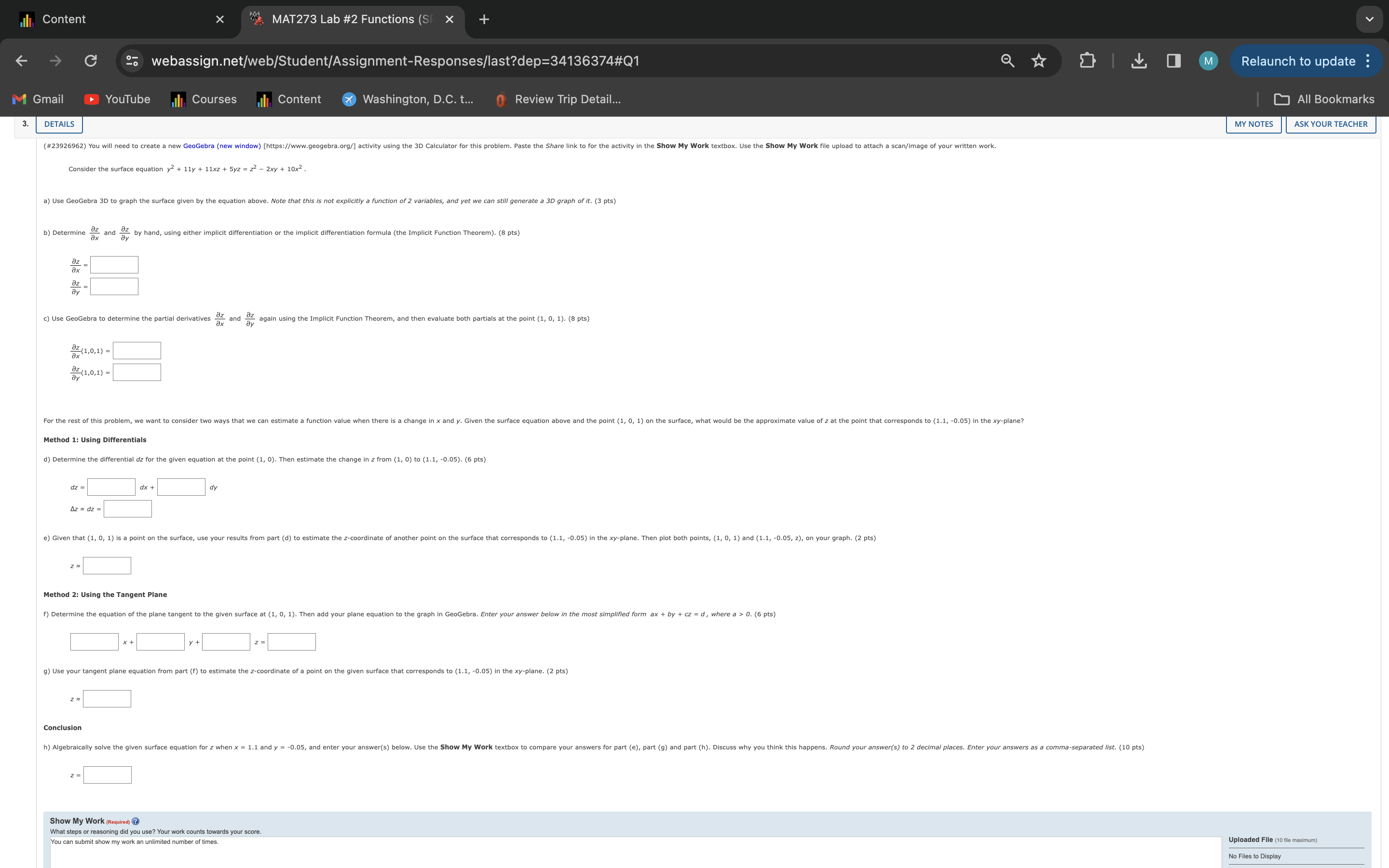
N LIS "k MAT273 Lab #2 Functions (S X + = ) 25 webassign.net/web/Student/Assignment-Responses/last?dep=34136374#Q1 (el > YouTube Il Courses |, Content @& Washington, D.C. t... Review Trip Detail... Current Score QUESTION 1 2 3 @ Instructions ~ The purpose of this lab is to help you explore differential calculus of functions in 3D space using GeoGebra. You have 3 submissions for each part/answer, but this is only to account for accidental submissions or if you find errors in your work while checking it after finished. You will not receive feedback on any submission during the lab, and only the last submission for each part will count toward your grade. As with a test, you will not receive full credit if you have no work and any answer left blank in WebAssign will not receive points. Any answer submitted that has 0 supporting work will get 0 points. Any handwritten work should be scanned/photo and submitted using the file upload of the Show My Work section of each problem. In order to save and share your GeoGebra work, you will need to create a free GeoGebra account. For each problem, create a new GeoGebra document. Paste the Share link to each GeoGebra document in the Show My Work textbox. If you have any technical issues with the lab, such as uploading pictures, please email your instructor (jmbowers@waketech.edu). Academic Integrity: You are welcome to work on the lab with classmates, but be sure you are submitting your own work. Please do not post your work/solutions in the weekly forum and do not post any part of your lab to online forums or websites such as Chegg (if a copy of any part of your lab is found online, it will be considered as cheating and result in a 0 on the lab). Assignment Submission & Scoring Assignment Submission Relaunch to update : [ All Bookmarks Due Date FRI, FEB 23, 2024 11:59 PM EST Request Extension For this assignment, you submit answers by question parts. The number of submissions remaining for each question part only changes if you submit or change the answer. Assignment Scoring Your last submission is used for your score. ASK YOUR TEACHER (#53591513) Open a browser and navigate to GeoGebra (new window) [https://www.geogebra.org/]. You will need to create a new activity using the 3D Calculator for this problem. A free GeoGebra account is required to N LIS "k MAT273 Lab #2 Functions (S X + (&) 23 webassign.net/web/Student/Assignment-Responses/last?dep=34136374#Q1 Relaunch to update =55 [ All Bookmarks YouTube Il Courses |, Content @& Washington, D.C. t... Review Trip Detail... MY NOTES ASK YOUR TEACHER (#53591513) Open a browser and navigate to GeoGebra (new window) [https://www.geogebra.org/]. You will need to create a new activity using the 3D Calculator for this problem. A free GeoGebra account is required to save your activity for submission. Paste the Share link to for the activity in the Show My Work textbox. Use the Show My Work file upload to attach a scan/image of your written work. A couple things to consider. First, sometimes the graph will get overly filled up as you keep adding new inputs into the activity, so feel free to hide various parts by deselecting the item by clicking the little circle next to your input. Second, keep in mind that all technology has limitations. In the case of 3D graphing software, sometimes weird things happen visually in the graph due to how the curve or surface is generated by the software. Often, this is unavoidable. But you can use your knowledge of math and graphs of functions to realize when something weird is happening so that you can simply acknowledge it and work with it despite these shortcomings. Consider the function f(x,y) = xy? 4x% + 2y? + 16y + 11. a) Graph the given function using GeoGebra 3D. (3 pts) in later computations to GeoGebra Instructions: as the name of the function being graphed. You can then use You can specify the function name as you enter expressions into the command line. So by including the "f(x,y)" part at the beginning of your expression entered into the command line, GeoGebra will use the refer back to this function. b) Use GeoGebra to determine f, and f, . (6 pts) flxy) = fyx) = GeoGebra Instructions: Again, you can specify the function name as you enter expressions into the command line. For the partial derivative notation, type "f_x" to get the subscript x. Then use the Derivative(Function,Variable) command to compute the derivative. So to compute the partial derivative with respect to x, you would type "f_x = derivative(f,x)" into the command line. ) Determine algebraically all points (x, y) in the domain of f where f, and f, are both equal to 0. (Enter exact values. Enter your answers as a comma-separated list.) Note that this will be a system of non-linear equations that you need to solve by hand. (6 pts) ) d) Use GeoGebra to check your answers from part (c) by evaluating the partials at the points you found. (2 pts) GeoGebra Instructions: If you have been using the naming strategies describe in previous steps, then you can use the partial derivative names to compute these values. For example, if one of the points was (1, 2), then you could type "f_x(1,2)" and GeoGebra would compute the result. e) Compute the z-value for each point you found in (c) and plot the (x, y, z) coordinates on your graph. (Enter exact values. Enter your answers as a comma-separated list.) (4 pts) xy2) = f) Use GeoGebra to compute the second partial derivatives fy, and fy,, , and then use GeoGebra to evaluate both at each point you found in (c). (6 pts) Fadxy) = fyyxiy) = (S TCLT "Zk MAT273 Lab #2 Functions (S X e ) 25 webassign.net/web/Student/Assignment-Responses/last?dep=34136374#Q1 Relaunch to update YouTube | [T IR & Washington, D.C. t... Review Trip Detail... [ All Bookmarks ASK YOUR TEACHER (#42426280) You will need to create a new GeoGebra (new window) [https://www.geogebra.org/] activity using the 3D Calculator for this problem. Paste the Share link to for the activity in the Show My Work textbox. Use the Show My Work file upload to attach a scan/image of your written work. InG2 + y? + 1 Consider the function g(x,y) = & = =2 - Xy a) Graph the given function using GeoGebra 3D. (3 pts) b) Use GeoGebra to determine gy and gy . (6 pts) GeoGebra Instructions: The partial derivatives for this problem are rather complicated, which can cause the graph to lag really badly. To help keep your activity running smoothly, click the circle to the left of each partial derivative to deselect it from graphing. Only the g(x,y) function should be visible on the graph. ) Use GeoGebra to evaluate g, gy, and g, at the point (1, -1). Round your answers to 2 decimal places. Then plot the point (1, -1, z) on your graph, where z is your rounded value of g(1, -1). (3 pts) g(1,-1) = gx(1,-1) = gy(1,-1) = d) Determine the equation of the plane tangent to g at (1, -1) using the rounded values from (c). Then add your plane equation to the graph in GeoGebra. Enter your answer in the simplified form ax + by + cz = d_given below, where d > 0. (6 pts) &) Use the Show My Work textbox to describe how the graph of the function, point, and plane are related to each other. Does the completed graph show what you would have expected based on your work above? (4 pts) Show My Work equres) @ What steps or reasoning did you use? Your work counts towards your score. You can submit show my work an unlimited number of times. Uploaded File (10 file maximum) No Files to Display ) Upload File Show My Work has not been graded yet. Uploaded File (10 fle maximum) No Files to Display Submit Answer Content X "A MAT273 Lab #2 Functions (SF 20 webassign.net/web/Student/Assignment-Responses/last?dep=34136374#Q1 Relaunch to update : M Gmail YouTube il Courses lil Content * Washington, D.C. t... 0 Review Trip Detail... All Bookmarks 3. DETAILS MY NOTES ASK YOUR TEACHER (#23926962) You will need to create a new GeoGebra (new window) [https://www.geogebra.org/] activity using the 3D Calculator for this problem. Paste the Share link to for the activity in the Show My Work textbox. Use the Show My Work file upload to attach a scan/image of your written work. Consider the surface equation y2 + 1ly + 11xz + 5yz = z2 - 2xy + 10x2. a) Use GeoGebra 3D to graph the surface given by the equation above. Note that this is not explicitly a function of 2 variables, and yet we can still generate a 3D graph of it. (3 pts) b) Determine and 2 by hand, using either implicit differentiat or the implicit differentiation formula (the Implicit Function Theorem). (8 pts) oz az c) Use GeoGebra to determine the partial derivatives or and 2% again using the Implicit Function Theorem, and then evaluate both partials at the point (1, 0, 1). (8 pts) oz (1,0,1) oz (1,0,1) = For the rest of this problem, we want to consider two ways that we can estimate a fun hen there is a change in x and y. Given the surface equation above and the point (1, 0, 1) on the surface, what would be the approximate value of z at the point that corresponds to (1.1, -0.05) in the xy-plane? Method 1: Using Differentials d) Determine the differential dz for the given equation at the point (1, 0). Then estimate the change in z from (1, 0) to (1.1, -0.05). (6 pts) dz = dx + Az = dz = e) Given that (1, 0, 1) is a point on the surface, use yo ponds to (1.1, -0.05) in the xy-plane. Then plot both points, (1, 0, 1) and (1.1, -0.05, z), on your graph. (2 pts) Method 2: Using the Tangent Plane f) Determine the equation of the plane tangent to the given surface at (1, 0, 1). Then add your plane equation to the graph in GeoGebra. Enter your answer below in the most simplified form ax + by + cz = d, where a > 0. (6 pts) 9) Use your tangent plane equation from part (f) to estimate the z-coordinate of a point on the given surface that corresponds to (1.1, -0.05) in the xy-plane. (2 pts) Conclusion h) Algebraically solve the given surface equation for z when x = 1.1 and y = -0.05, and enter your answer(s) below. Use the Show My Work textbox to compare your answers for part (e), part (9) and part (h). Discuss why you think this happens. Round your answer(s) to 2 decimal places. Enter your answers as a comma-separated list. (10 pts) Show My Work (Required) @ What steps or reasoning did you use? Your work counts towards your score. an submit show my work an unlimited number of times. Uploaded File (10 file maximum) No Files to Display