Question: n Use induction to prove: for any integer n 1, (6j 4) = 3n n. - j=1 Base case n = Inductive step (6j

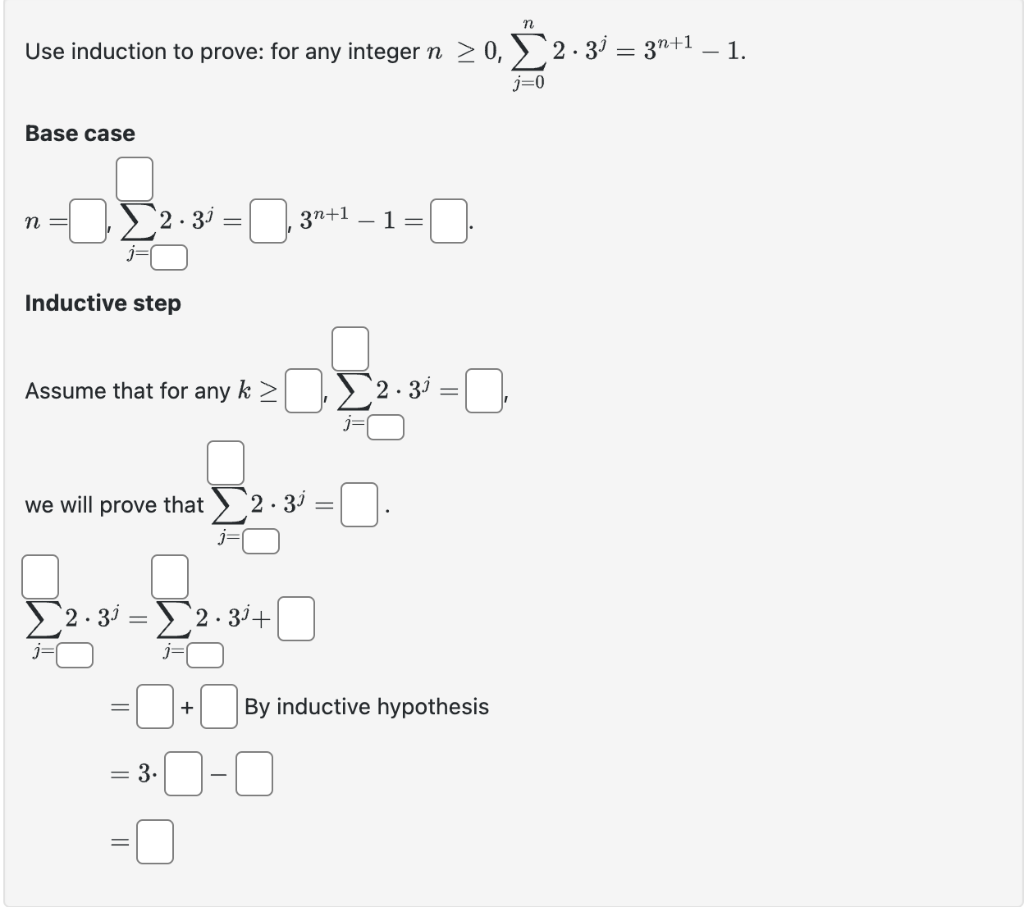
n Use induction to prove: for any integer n 1, (6j 4) = 3n n. - j=1 Base case n = Inductive step (6j - 4) = , 3n Assume that for any k , (6j 4) = we will prove that (6j 4) = WI (6j 4) = (6j 4)+| FO = = = 3 + -n= + k+ +k+) (k+1) -(k+1) k. By inductive hypothesis Use induction to prove: for any integer n > 0, 2.3 = 3*+1 1. j=0 Base case 2.3 = C 3n+1 Inductive step Assume that for any k > 2.3 we will prove that 2.30 - = 2.3 - 2.3+ j=1 j= = 3. -1= + By inductive hypothesis

Step by Step Solution

★★★★★

3.40 Rating (156 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Date1 To prove For ny 1 Base case A 2 6f4 6j4 61 Y 64 11 87 n 11 4 pr... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Use induction to prove the summation formulae (1.60). (1.61) and (1.62). n-n multiplications and J- 1 additions. j-1 j=1 multiplications, along with j-1 (n-j) = additions i-1

In this question we study the recursively defined functions f, g and h given by the following defining equations f(0) = 1 base case 0, f(1) = 0 base case 1, and f(n) = n f(n 1) + f(n 2)^2...

Safe Pharmaceutical Company is engaged in manufacturing of life saving medicines. In order to avoid multiple panels of wholesale dealers for distribution of its medicines, the company has registered...

For the following exercises, use the Binomial Theorem to expand the binomial f(x) = (x + 3) 4 .Then find and graph each indicated sum on one set of axes. Find and write the answer as a binomial...

1, Let be an angle defined on a unit circle, and is the point on this circle defined by , see the picture to the right. Recall also that the angle determining the full circle is 360 (360 degrees)....

Let be an eigenvalue of the n n matrix A and x = 0 be an associated eigenvector. a. Show that is also an eigenvalue of At. b. Show that for any integer k 1, k is an eigenvalue of Ak with...

What is the sum of all the even numbers from 0 to 2n, for any integer n 1?

Determine whether the following statements are true and give an explanation or counterexample. a. d/dx (e 5 ) = 5e 4 . b. The Quotient Rule must be used to evaluate d/dx (x 2 + 3x + 2/x). c. d/dx...

12. Using part (d) of Exercise 8 show that for any integer n, (dl2n + 1 and dln 2 + 3n + 1) =? dl5n + 2, and then that (dl2n + 1 and dl5n + 2) ==> dll. Deduee that ged(n2 + 3n + 1, 2n + 1) = l.

If T has geometric distribution with , i.e. P(T = i) = (1 ) i1 for any integer i = 1, 2, . . ., what are the expressions of S(t), (t), (t) and m(t)?

Exercise 4 - 3 ( Algo ) Compute ABC Product Costs [ LO 4 - 3 ] Larner Corporation is a diversified manufacturer of industrial goods. The company's activity - based costing system contains the...

you should draft a description of the project ((project name Marketing for the Clubs Hubspot))and an initial write up of your stakeholders - identify the stakeholders. For each stakeholder and/or...

Thinking of a manufacturing company, how might probability be a part of their quality control? Which companies might consider more outcomes as "unusual" based on the sensitivity of what they produce?...

Indicate if the following statements are true (T) or false (F): 1. Question 1 The efficient frontier will always contain the cheapest company in the industry. 2 points True False 2. Question 2 There...

On the Capella library's website on selecting a database, they provide an overview of the databases available through the university library. There are certain collections that are considered _______...

The question "What is the organization's mission?" is most closely tied to which task below? Question 7Answer a. Assess relationships with revenue sources. b. Search for cultural artifacts. c....

What are two applications of 3 D and 4 D printing?

1. True or False. Pitfalls to consider in a statistical test include nonrandom samples, small sample size, and lack of causal links. 2. Because 25 percent of the students in my morning statistics...

In Exercise 10.5.18 you were asked to solve a system by Gauss-Seidel. How much faster can you design an SOR scheme to converge? Experiment with several values of the relaxation parameter co, and...

Formulate conditions on a weight function «;(*) that guarantee that the weighted integral defines an inner product on the space of continuous complex-valued functions on [a. b]. (f. g)=|...

(a) Prove that the polynomials form an orthogonal basis for the vector space P3 of cubic polynomials for the L2 inner product (b) Find an orthonormal basis of V3. (c) Write t3 as a linear combination...

In preparation for significant international operations, ABC Co. has adopted a plan to gradually shift to the same accounting policies as used by its international competitors. Part of this plan...

As a public accountant, you have been contacted by Joe Davison, CEO of Sports-Pro Athletics, Inc., a manufacturer of a variety of athletic equipment. He has asked you how to account for the following...

Silva Rojas and Hans Jensen were discussing the statement of cash flows of Liu Ltd. In the notes to the statement of cash flows was a schedule entitled "Non-cash investing and financing activities."...