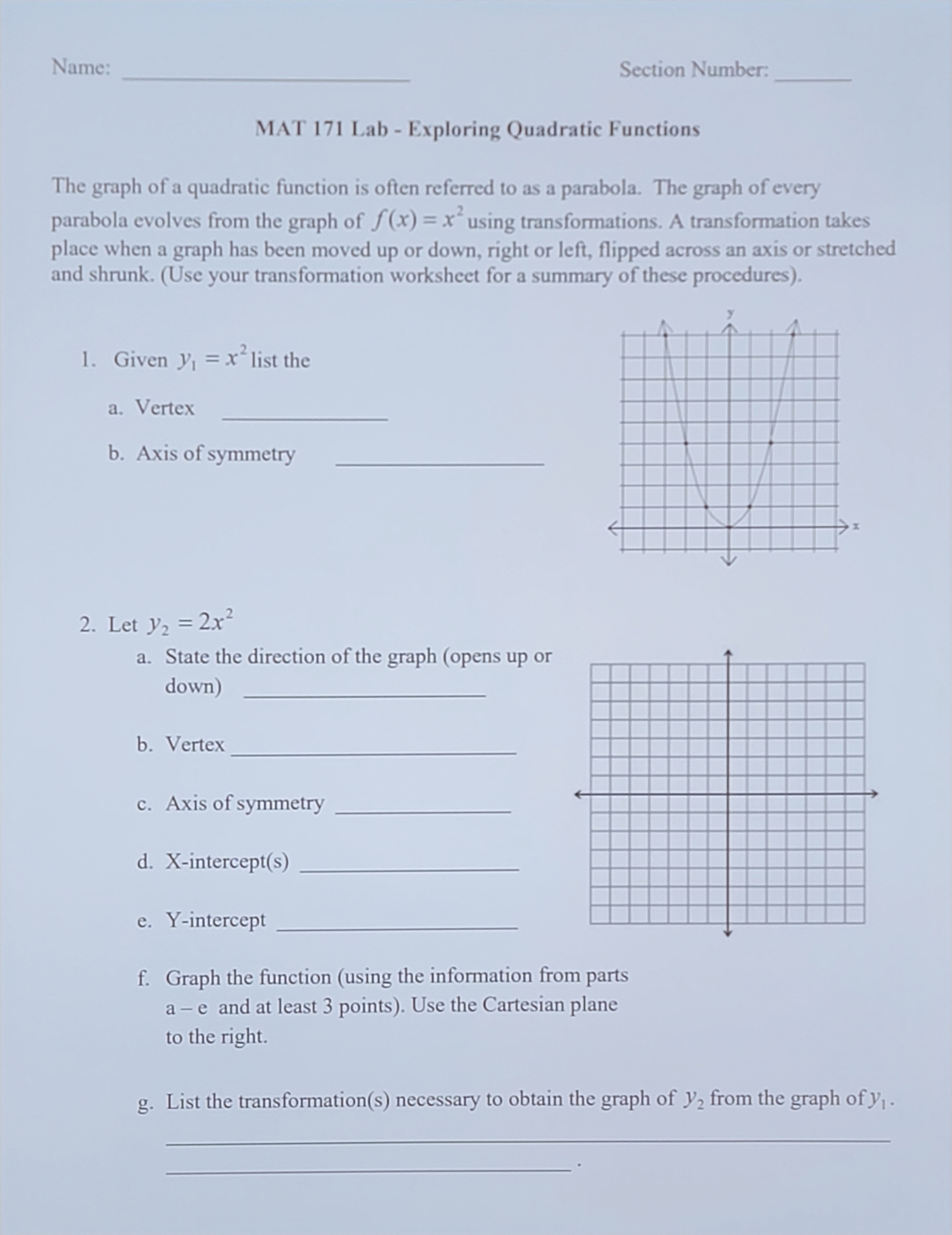
Name: Section Number: MAT 171 Lab - Exploring Quadratic Functions The graph of a quadratic function is often referred to as a parabola. The graph of every parabola evolves from the graph of f(x) = x using transformations. A transformation takes place when a graph has been moved up or down, right or left, flipped across an axis or stretched and shrunk. (Use your transformation worksheet for a summary of these procedures). 1. Given V1 = x list the a. Vertex b. Axis of symmetry 2. Let V2 = 2x2 a. State the direction of the graph (opens up or down) b. Vertex c. Axis of symmetry d. X-intercept(s) e. Y-intercept f. Graph the function (using the information from parts a - e and at least 3 points). Use the Cartesian plane to the right. g. List the transformation(s) necessary to obtain the graph of V2 from the graph of y1 -3. Let V3 = -2x2 a. State the direction of the graph (opens up or down) b. Vertex c. Axis of symmetry d. X-intercept(s) e. Y-intercept f. Graph the function (using the information from parts a-e and at least 3 points). Use the Cartesian plane to the right. g. List the transformation(s) necessary to obtain the graph of y3 from the graph of y1 - 4. Let yA = 2(x + 1) 2 a. State the direction of the graph (opens up or down) b. Vertex c. Axis of symmetry d. X-intercept(s) e. Y-intercept f. Graph the function (using the information from parts a-e and at least 3 points). Use the Cartesian plane to the right.g. List the transformation(s) necessary to obtain the graph of y4 from the graph of y1 . 5. Let ys = -2(x + 1)2 -4 a. State the direction of the graph (opens up or down) b. Vertex c. Axis of symmetry d. X-intercept(s) e. Y-intercept f. Graph the function (using the information from parts a-e and at least 3 points). Use the Cartesian plane to the right. g. List the transformation(s) necessary to obtain the graph of y3 from the graph of y1 . 6. Consider the graph of f (x) = a(x -h) +k . Using what you have learned from the graphs of V2, )3, V4 and y's, list the transformations necessary to obtain the graph of f (x) from the graph of V1. (You may assume that h and k are positive constants, but make sure to consider the two cases: 1) a > 0 and 2) a