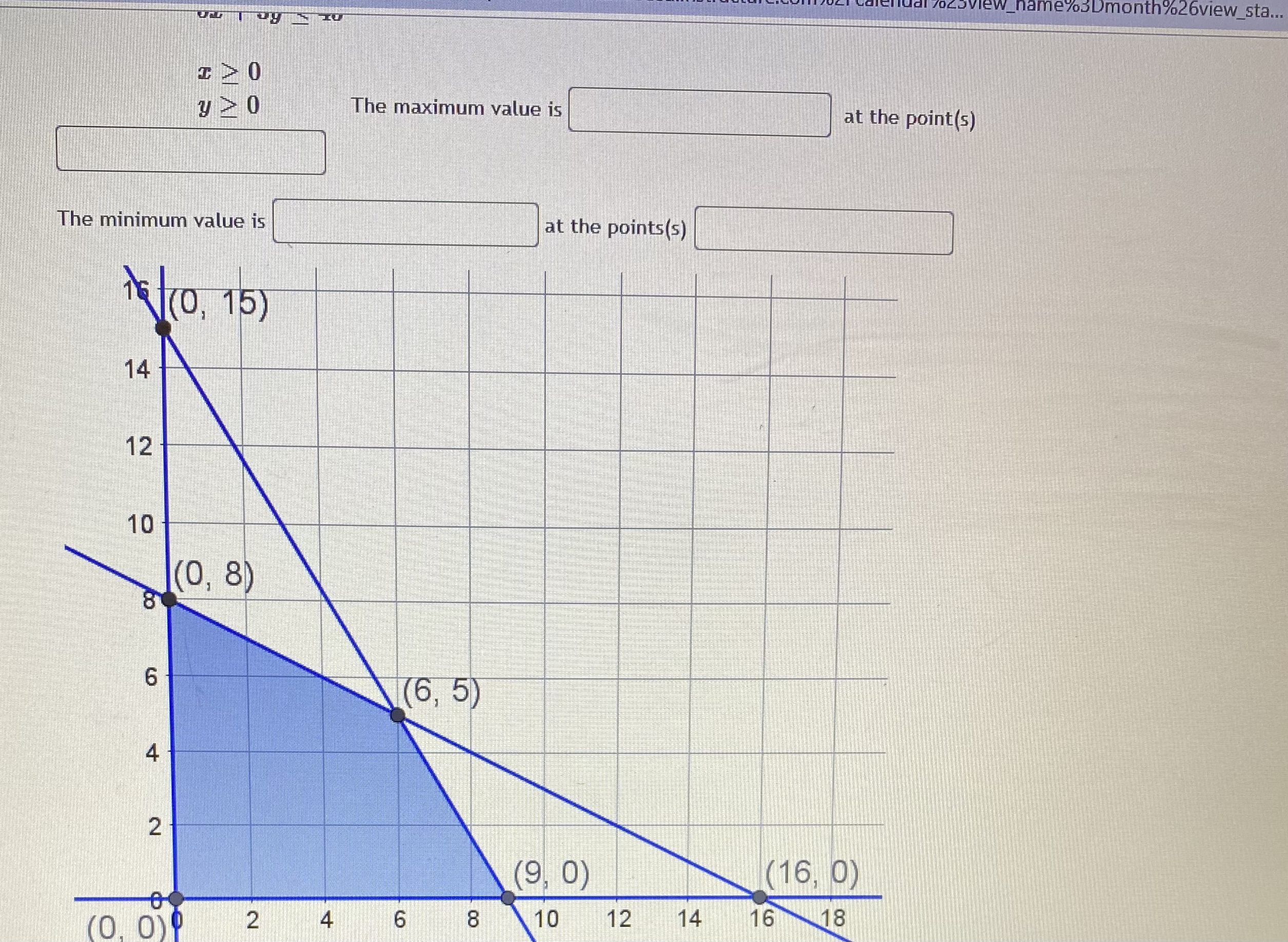
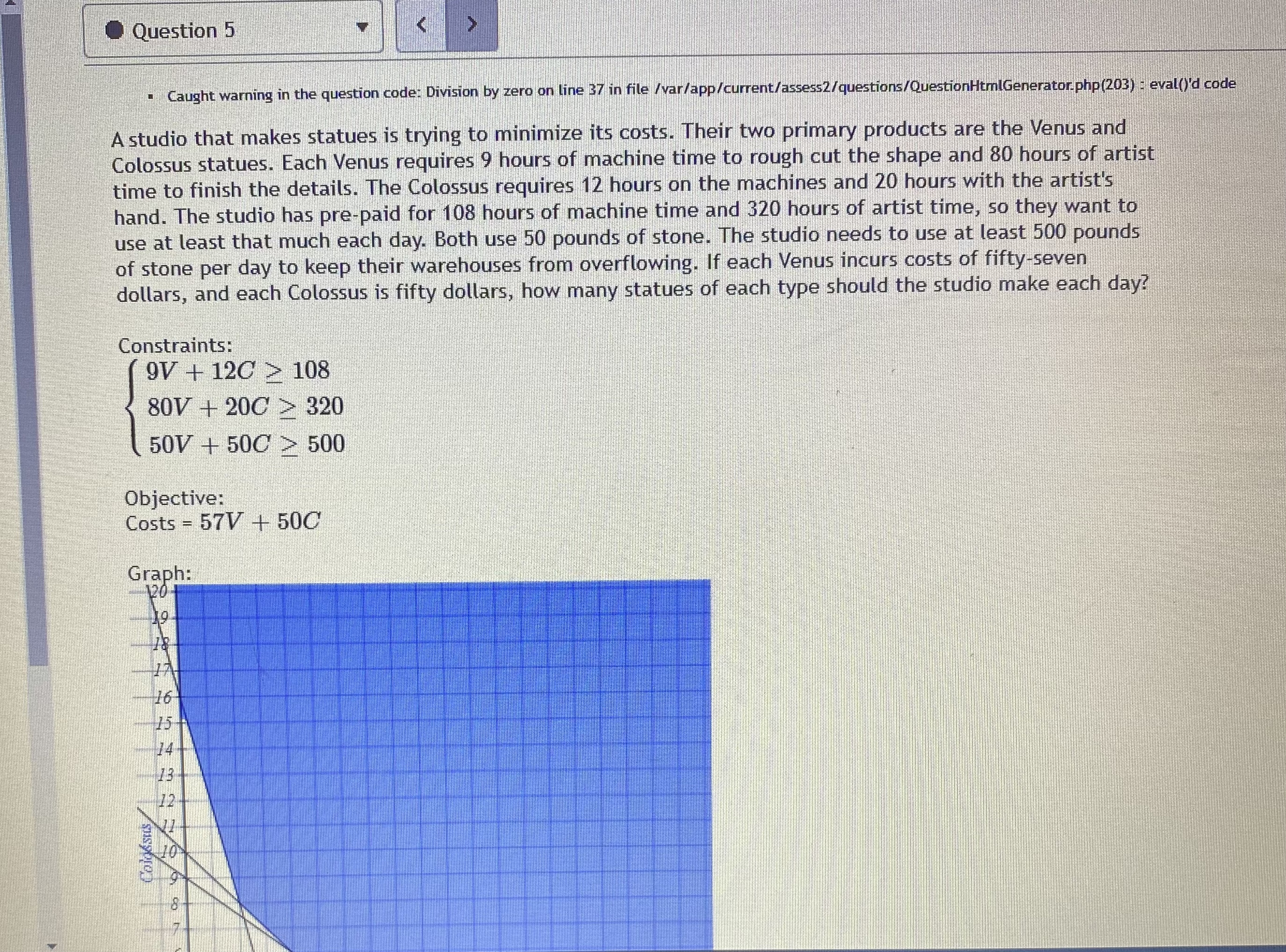
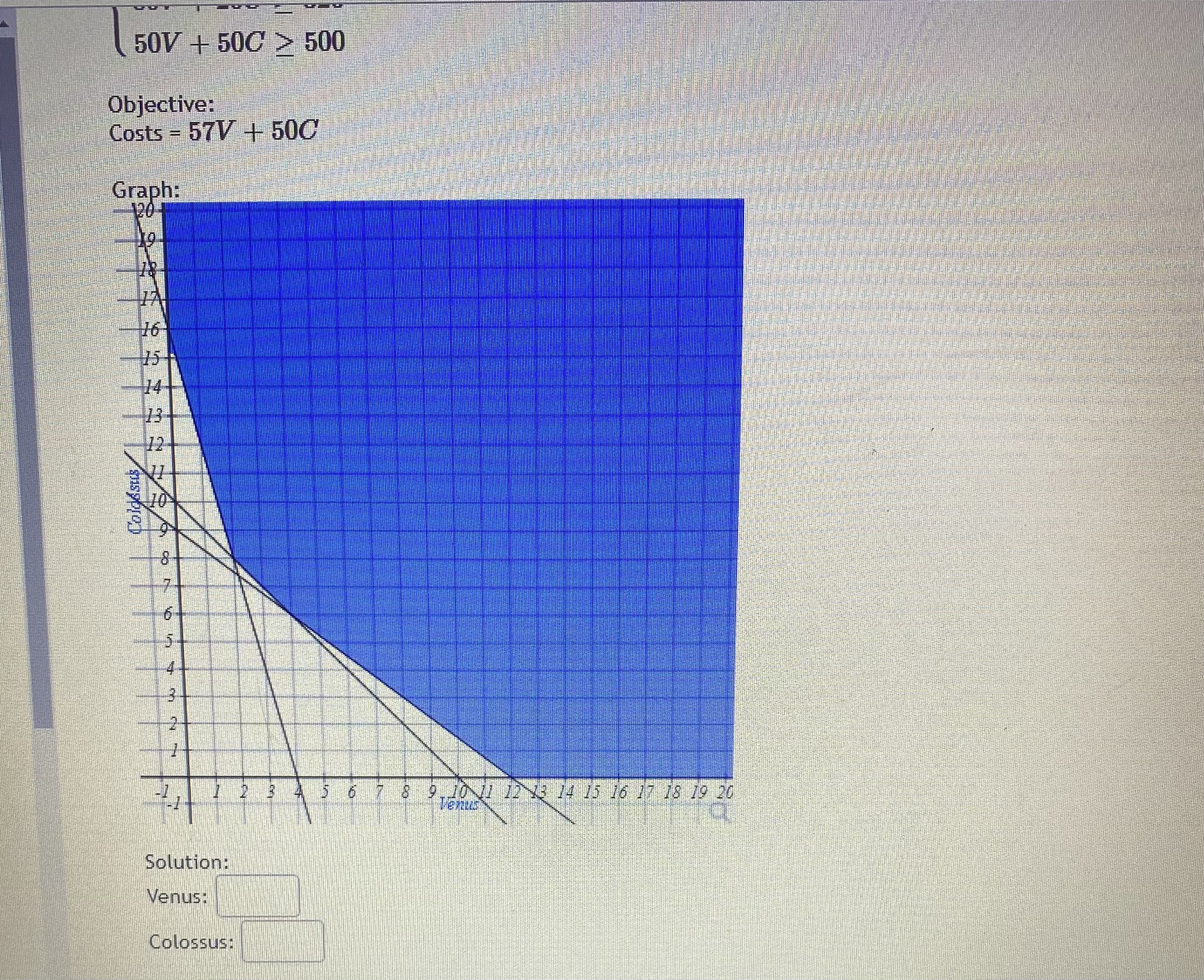
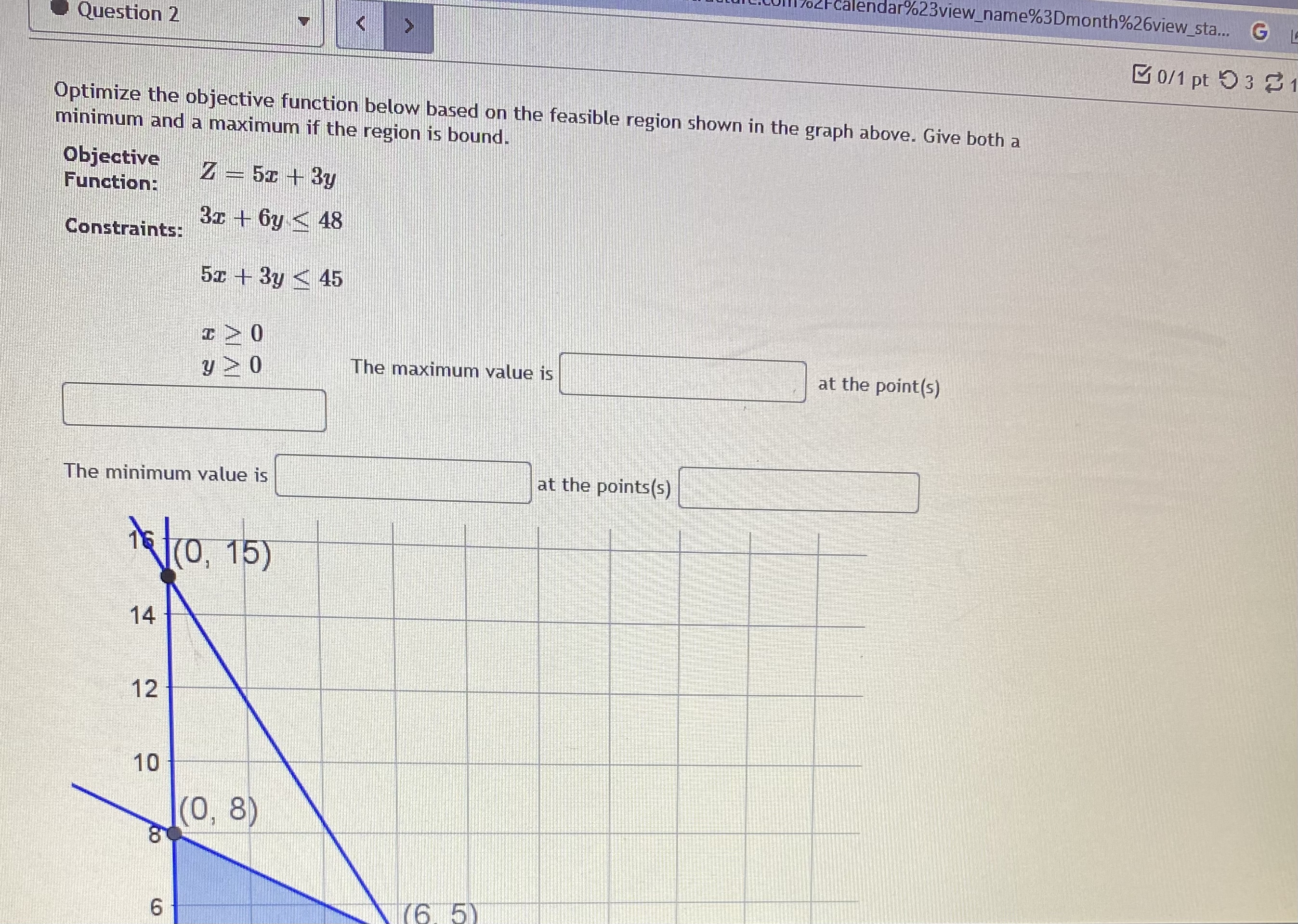
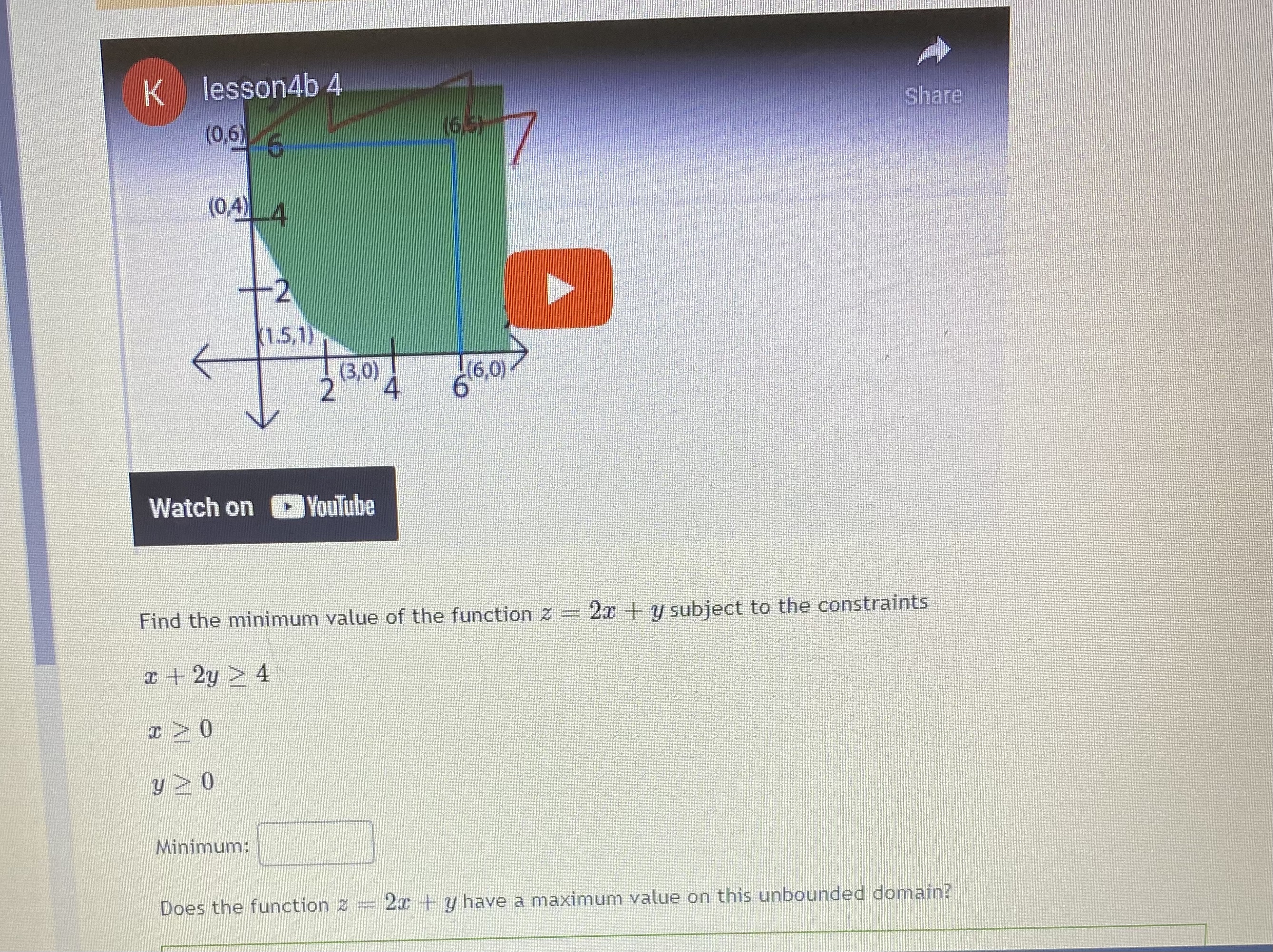
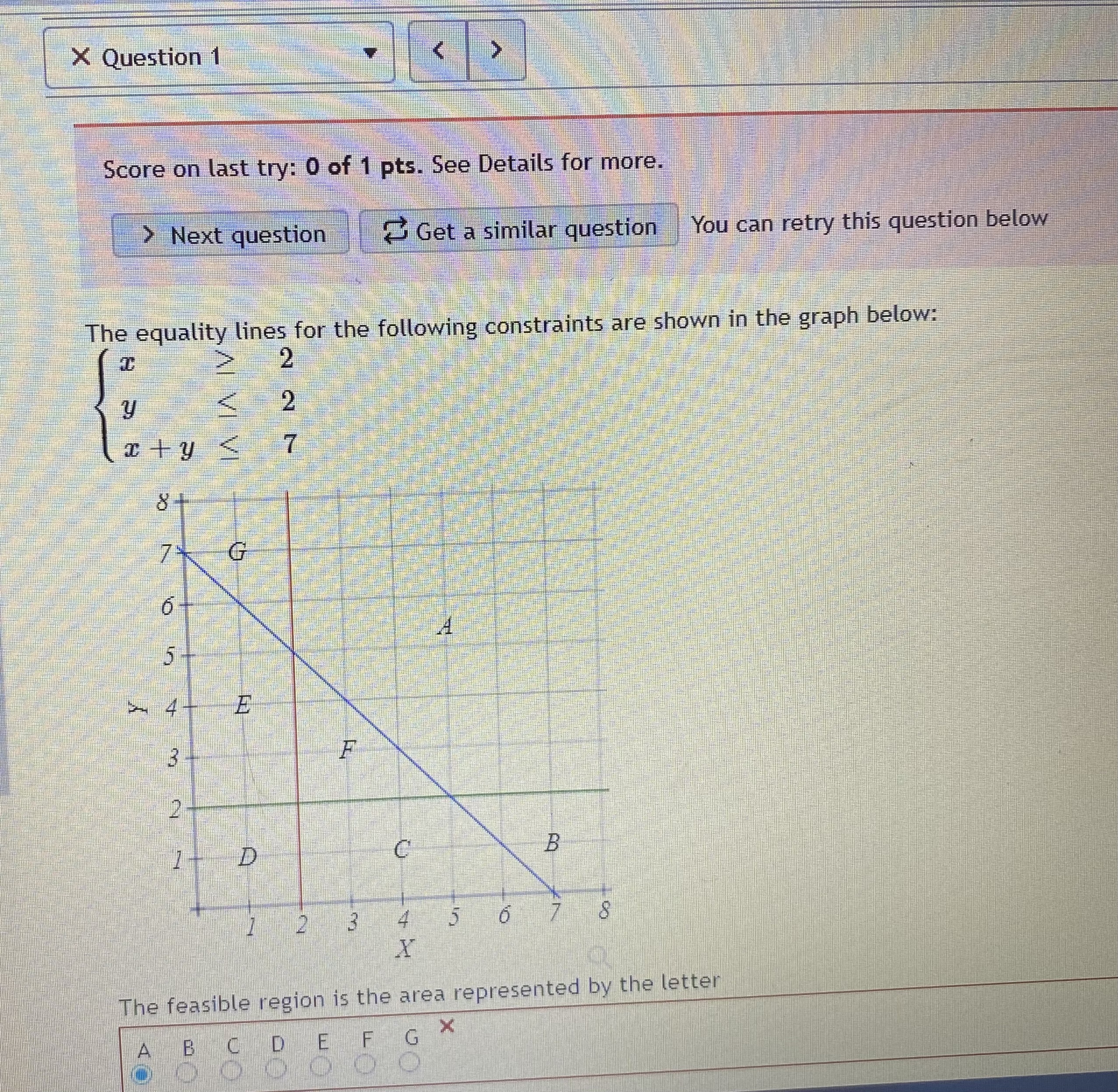
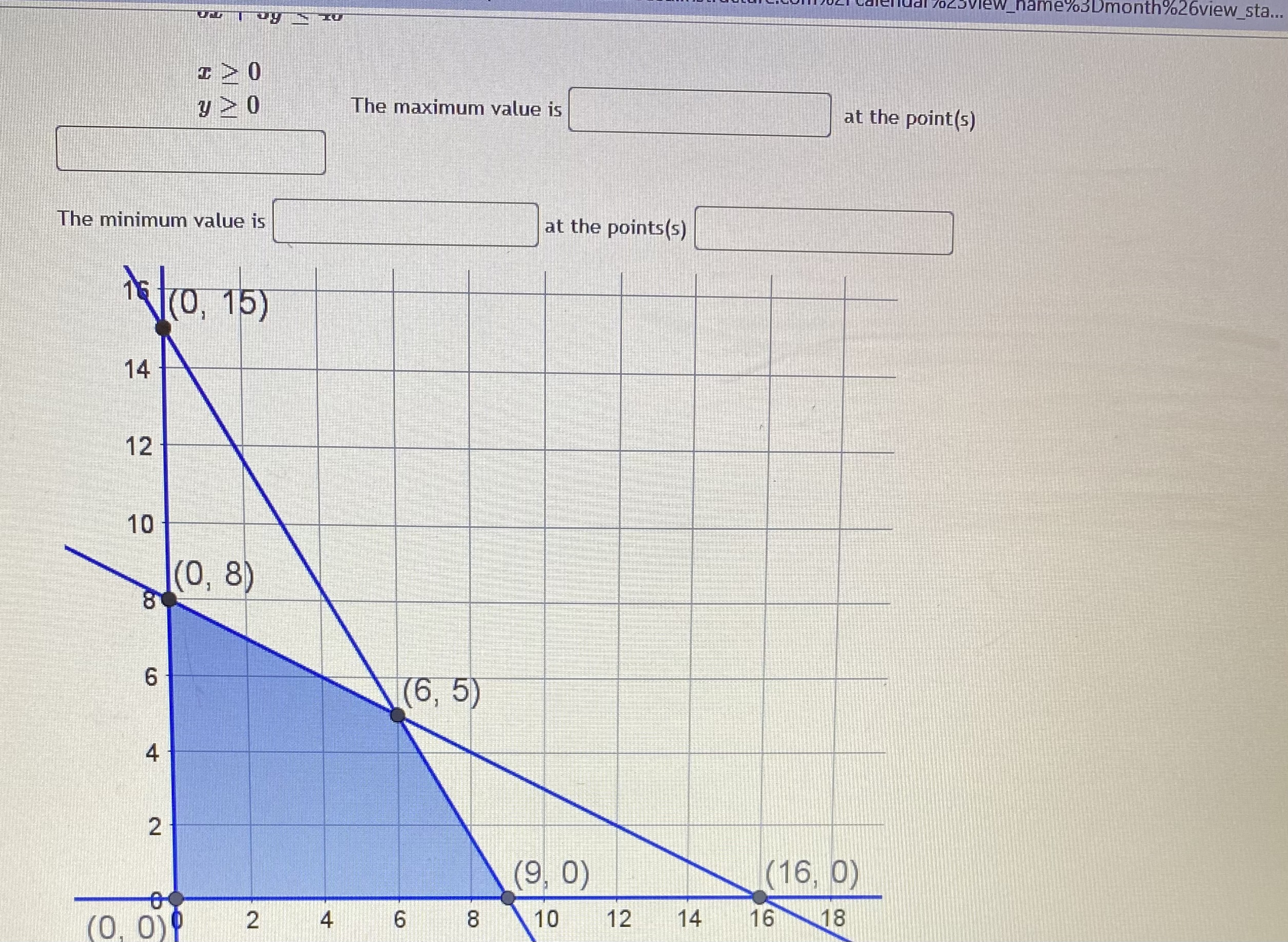
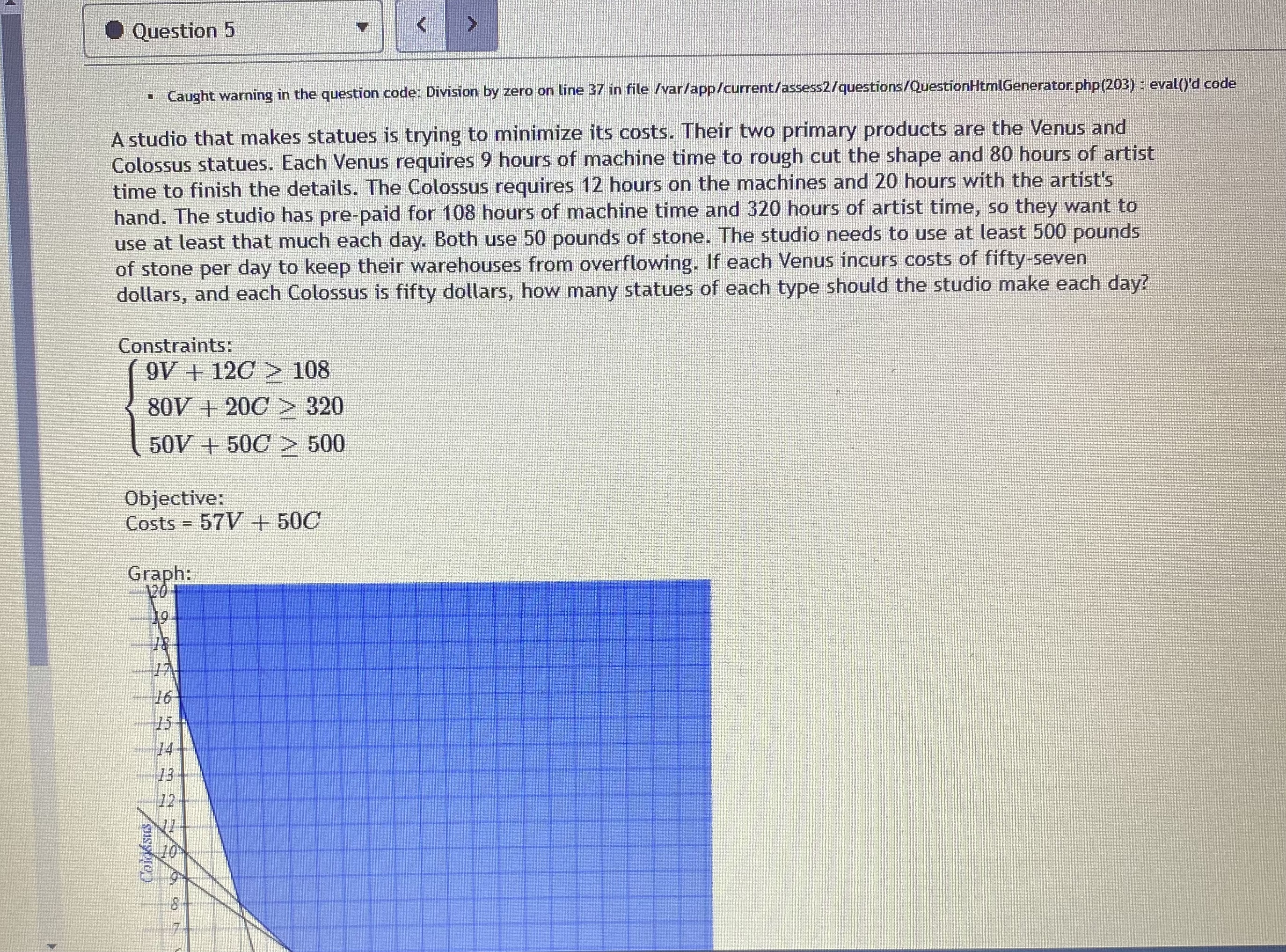
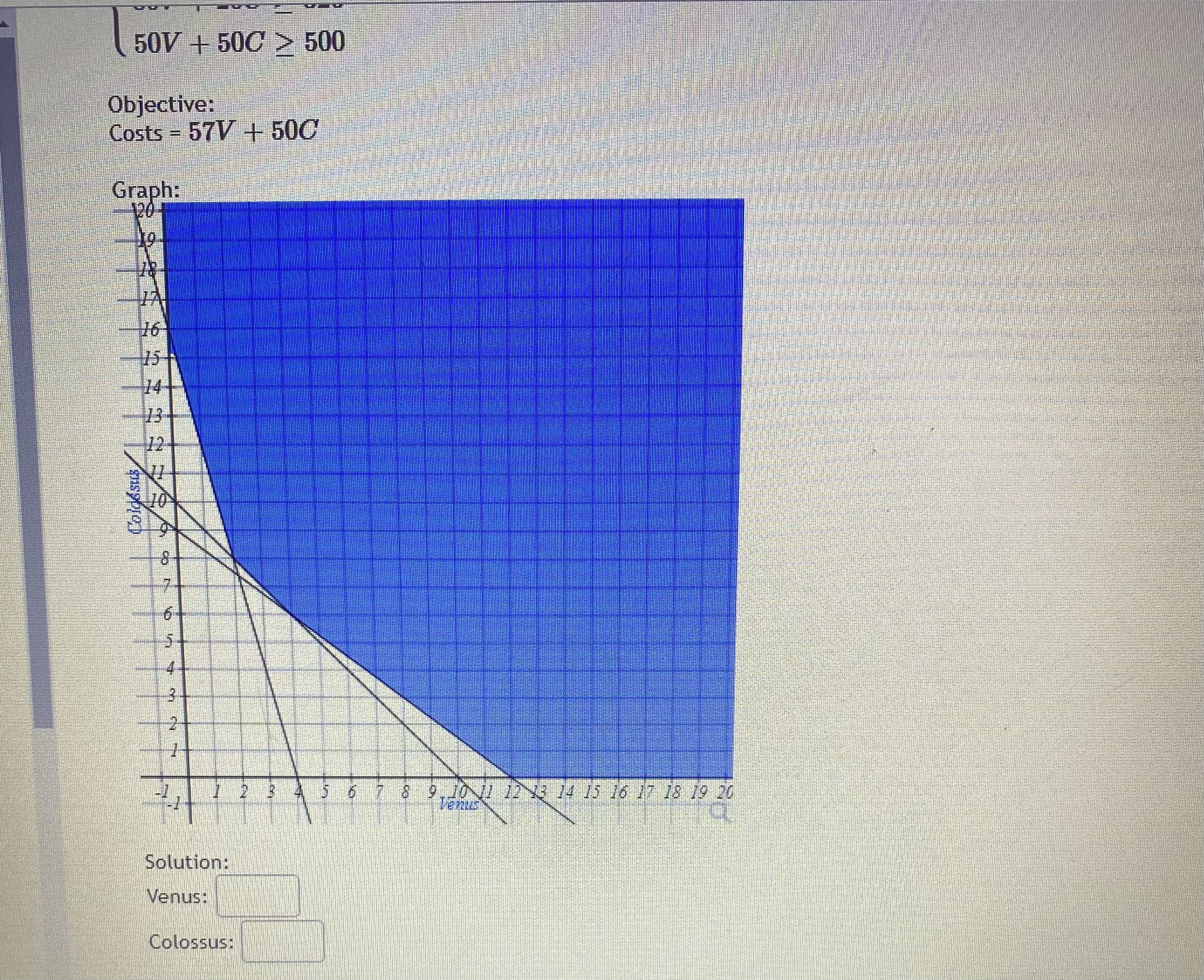
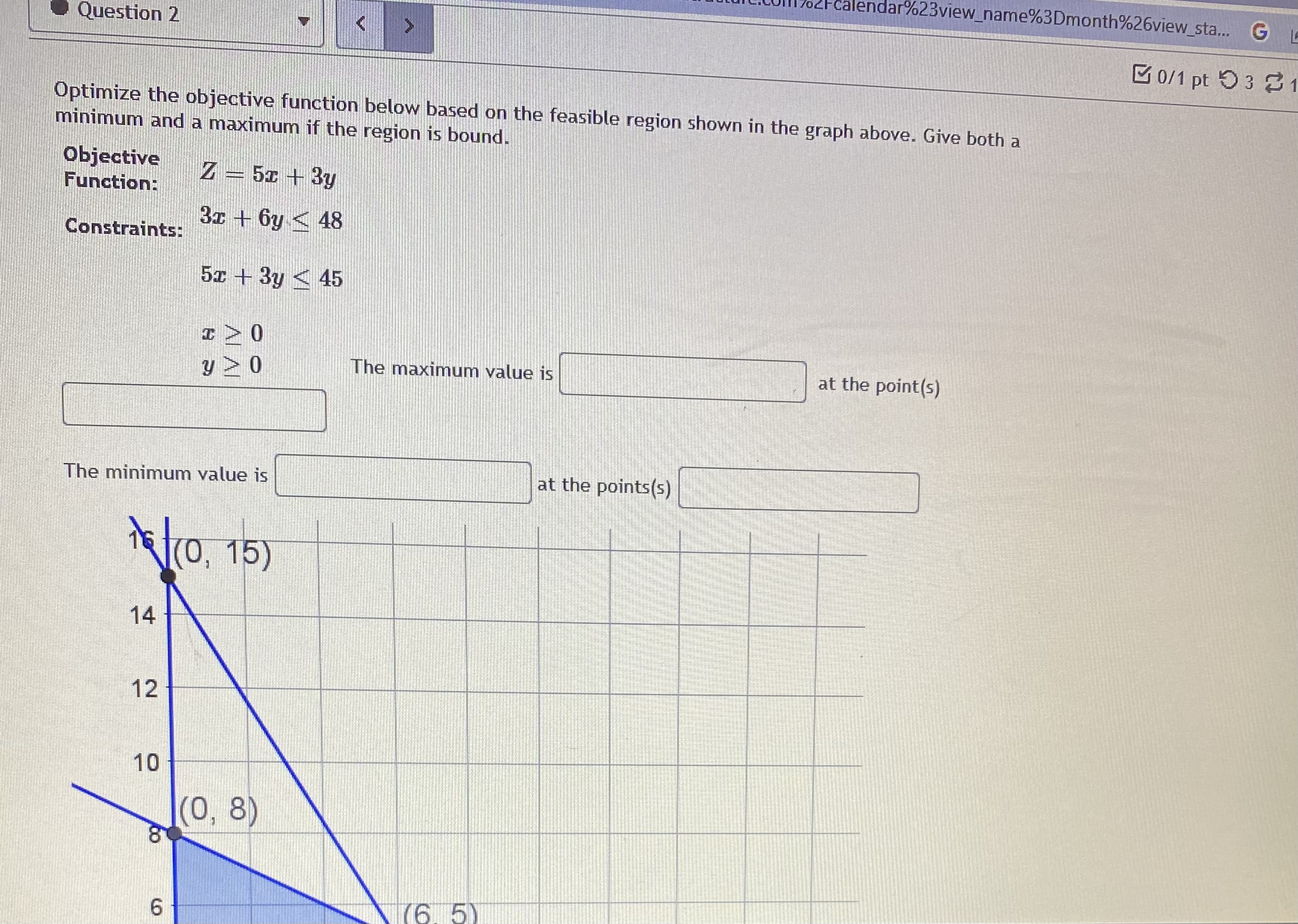
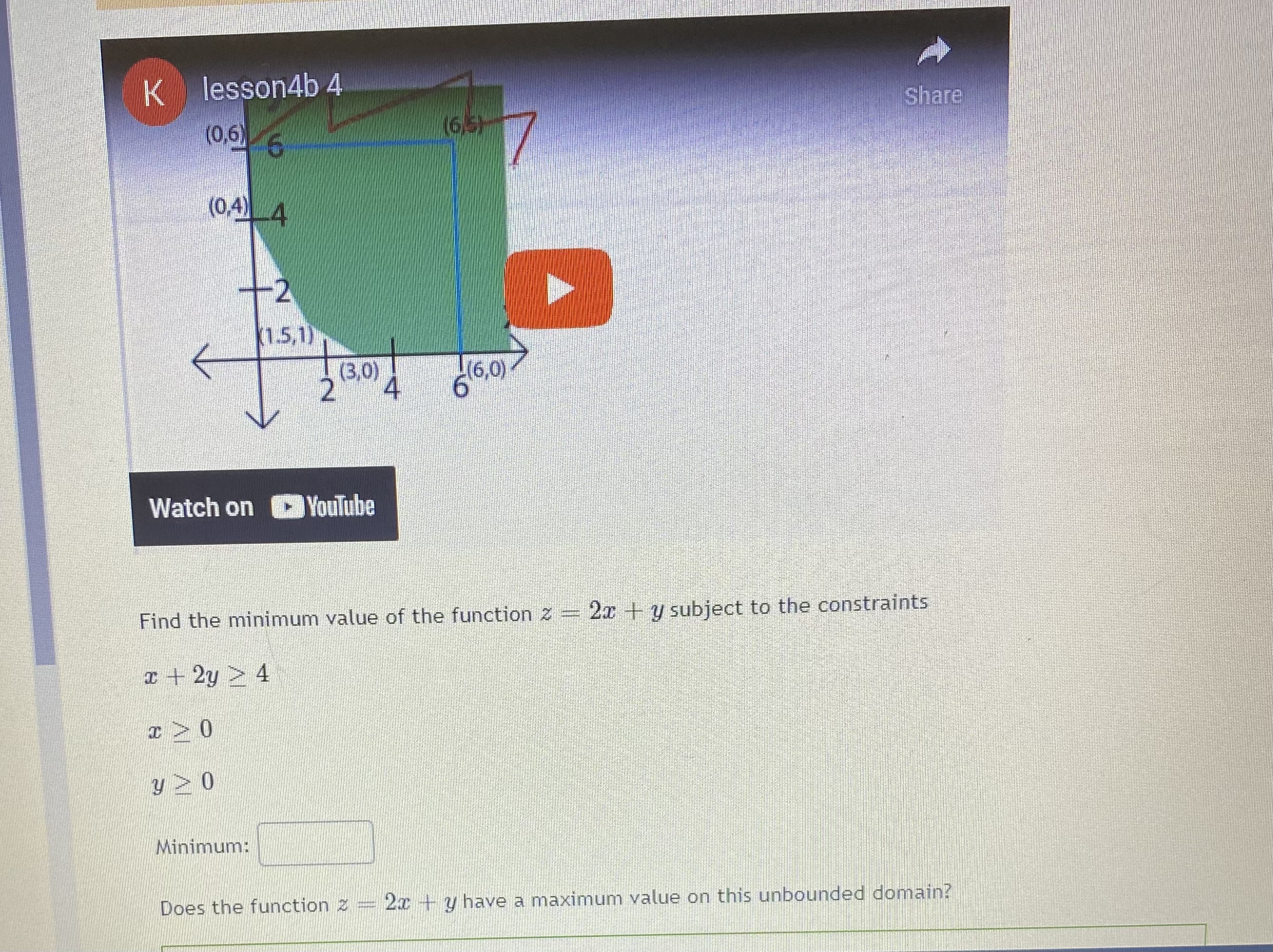
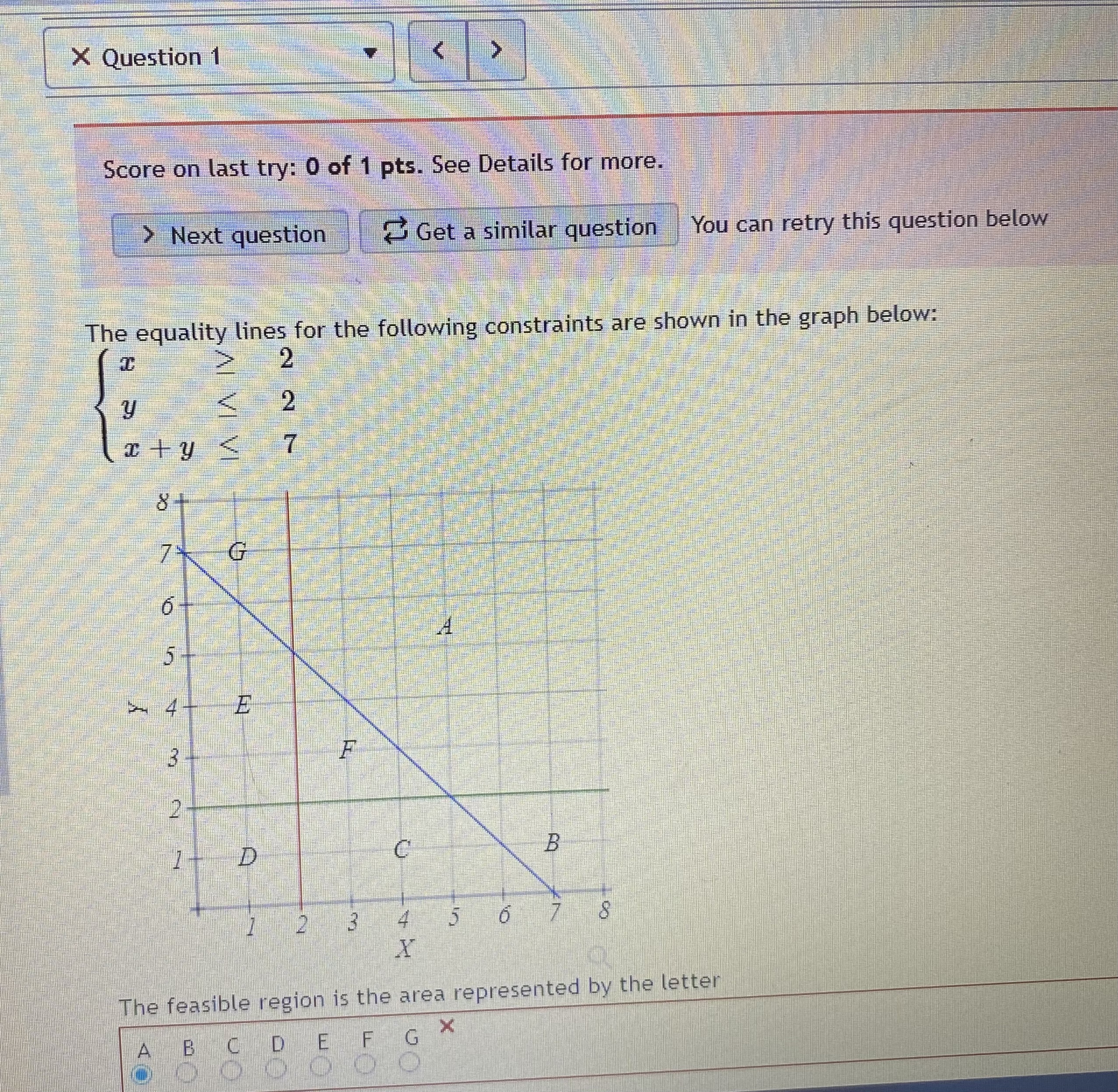
_name3Dmonth%26view_sta... 120 y>0 The maximum value is at the point(s) The minimum value is at the points(s) 1(0, 15 ) 14 12 10 1(0, 8) 8 6 (6, 5) 4 2 (9, 0) (16, 0) (0. 0)9 4 6 8 10 12 14 16 18Question 5 "Caught warning in the question code: Division by zero on line 37 in file / var/app/current/assess2/questions/QuestionHtmlGenerator.php(203) : eval()'d code A studio that makes statues is trying to minimize its costs. Their two primary products are the Venus and Colossus statues. Each Venus requires 9 hours of machine time to rough cut the shape and 80 hours of artist time to finish the details. The Colossus requires 12 hours on the machines and 20 hours with the artist's hand. The studio has pre-paid for 108 hours of machine time and 320 hours of artist time, so they want to use at least that much each day. Both use 50 pounds of stone. The studio needs to use at least 500 pounds of stone per day to keep their warehouses from overflowing. If each Venus incurs costs of fifty-seven dollars, and each Colossus is fifty dollars, how many statues of each type should the studio make each day? Constraints: (9V + 120 > 108 80V + 200 > 320 50V + 50C > 500 Objective: Costs = 57V + 500 Graph: 120 16 Colossus\f7ofcalendar%23view_name%3Dmonth%26view_sta... G Question 2 0/1 pt 9 3 3 Optimize the objective function below based on the feasible region shown in the graph above. Give both a minimum and a maximum if the region is bound. Objective Function: Z - 5 + 3y Constraints: 3x + 6y