Question: NEED A HELP WITH THE FOLLOWING QUESTION FOR CALCULUS YOU NEED TO ANSWER ALL QUESTIONS IF SOMEONE ANSWER NOT ALL THEN I WILL REPORT FOR
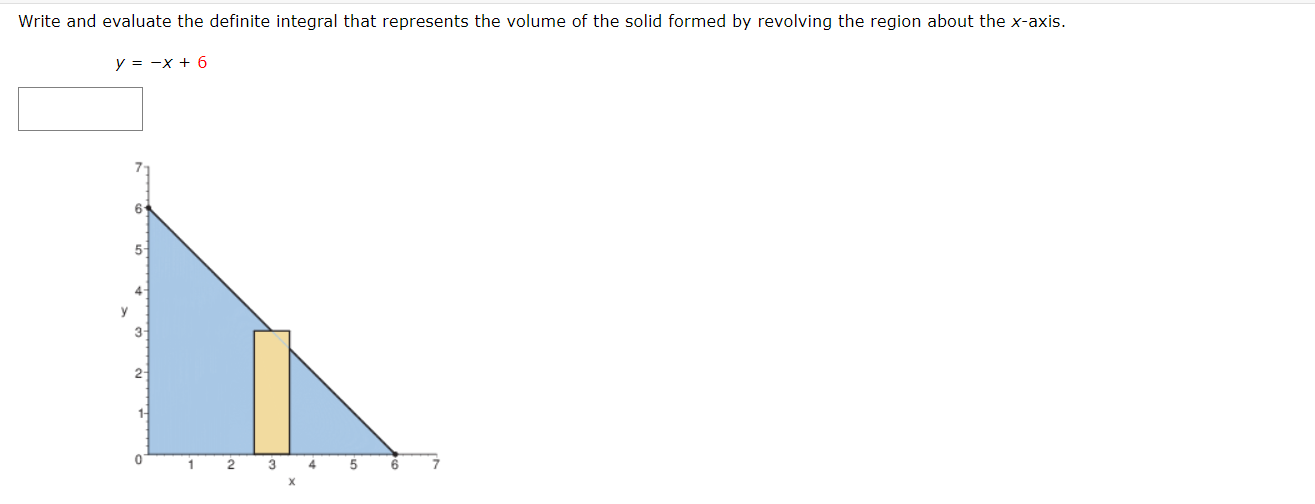


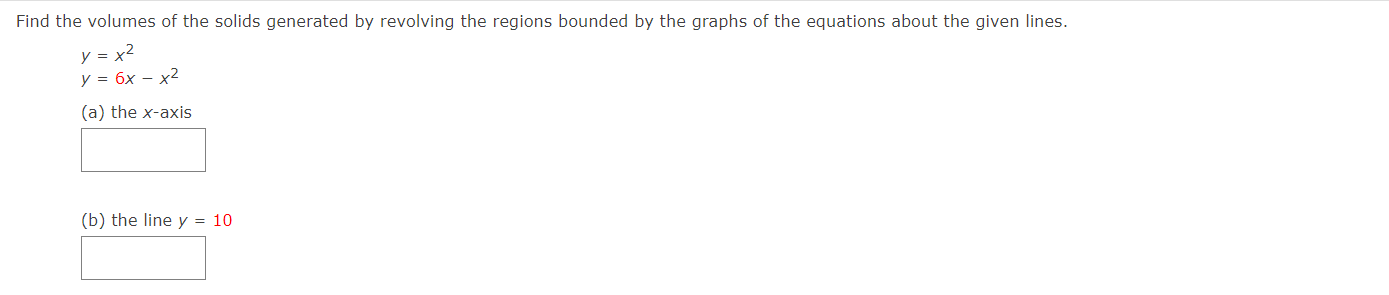

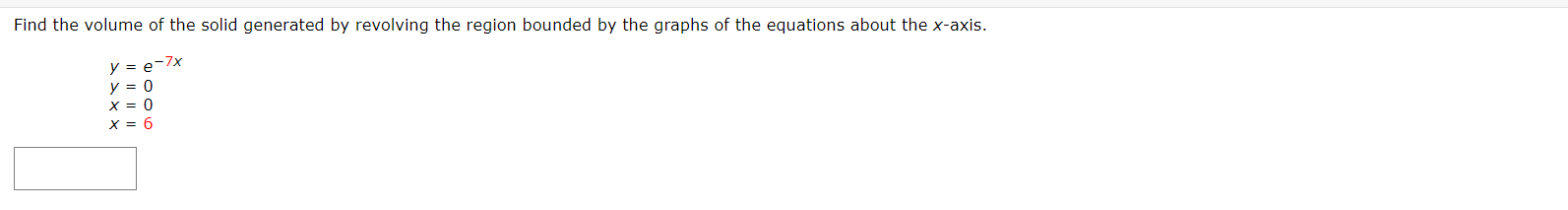
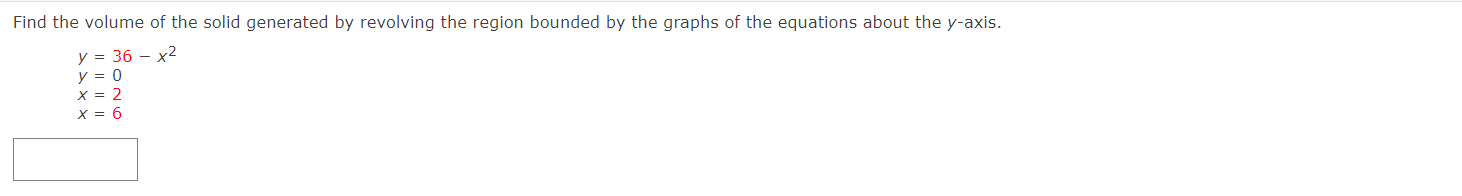










NEED A HELP WITH THE FOLLOWING QUESTION
FOR CALCULUS
YOU NEED TO ANSWER ALL QUESTIONS
IF SOMEONE ANSWER NOT ALL THEN
I WILL REPORT FOR IT
SO AS YOU KNOW THEN ANSWER ALL OF IT
THANKS
=
![L] 2 0.15 01 |:| IJL Use the shell method to write](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6660f0f0d5c4b_1686660f0f0c39fc.jpg)


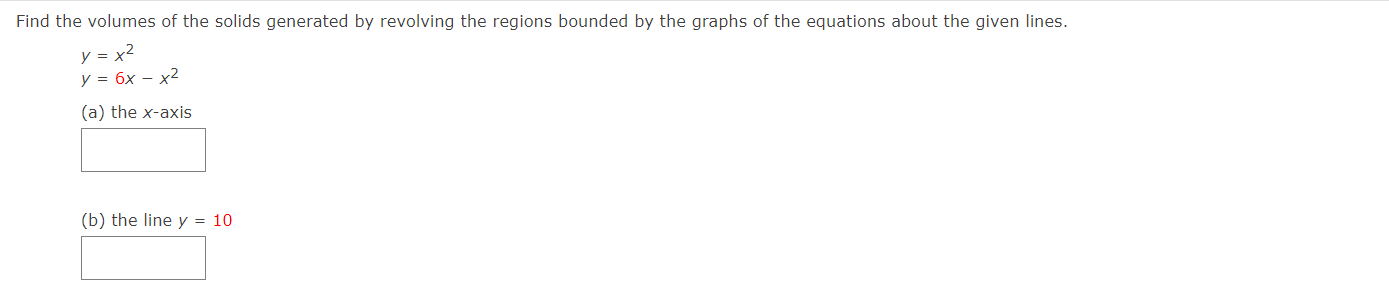

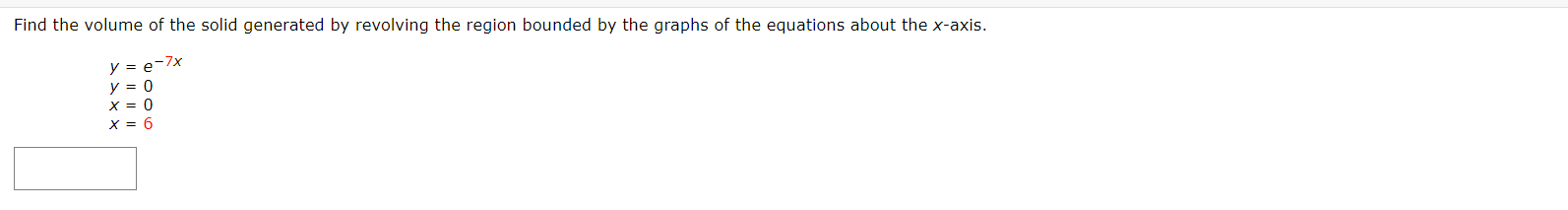
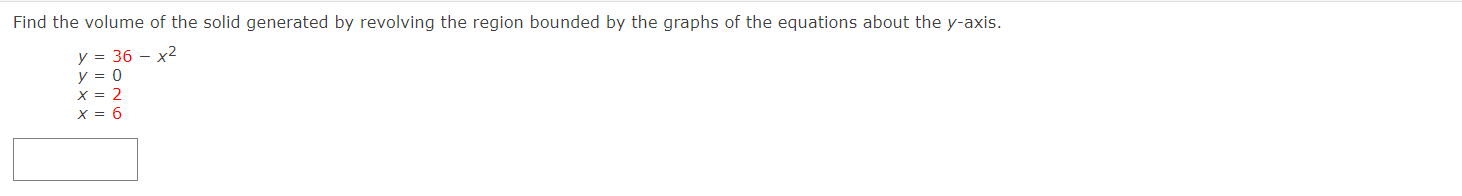
![represents the volume of a solid of revolution. 3 2"] x4 dx](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6660f0f309b86_1706660f0f2ebe94.jpg)

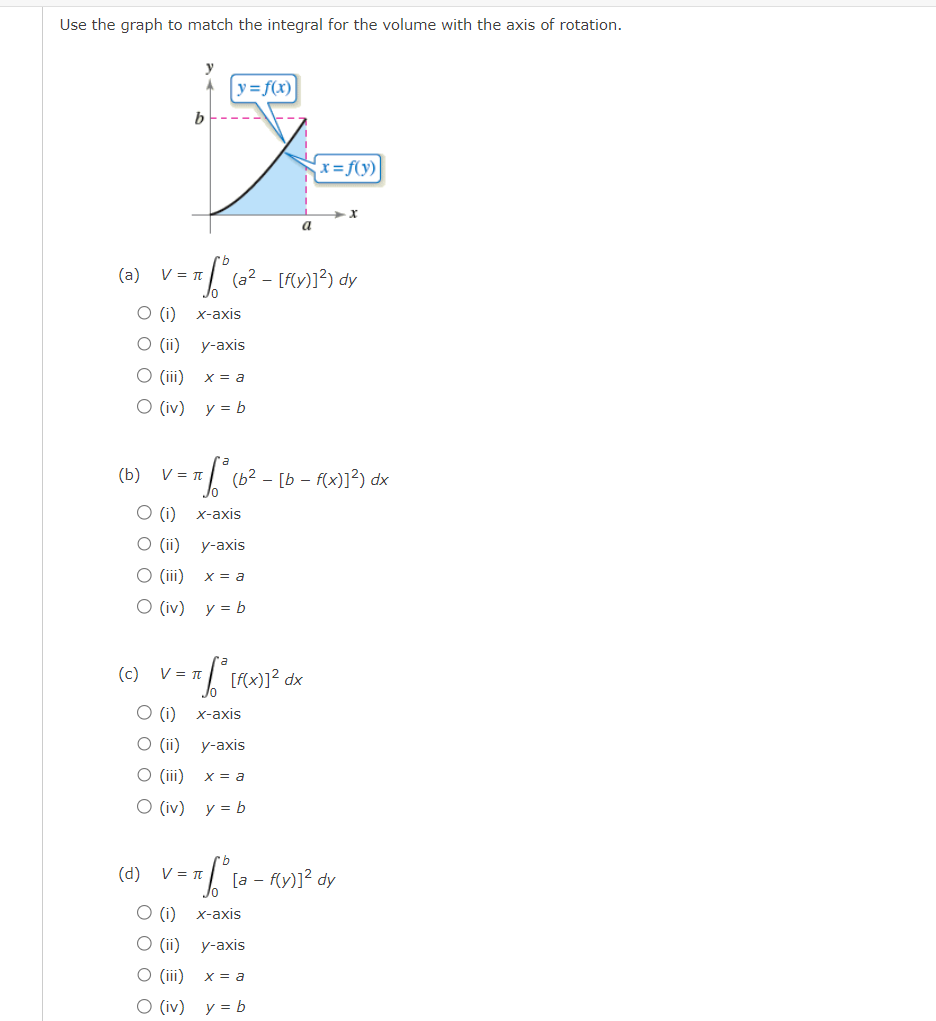




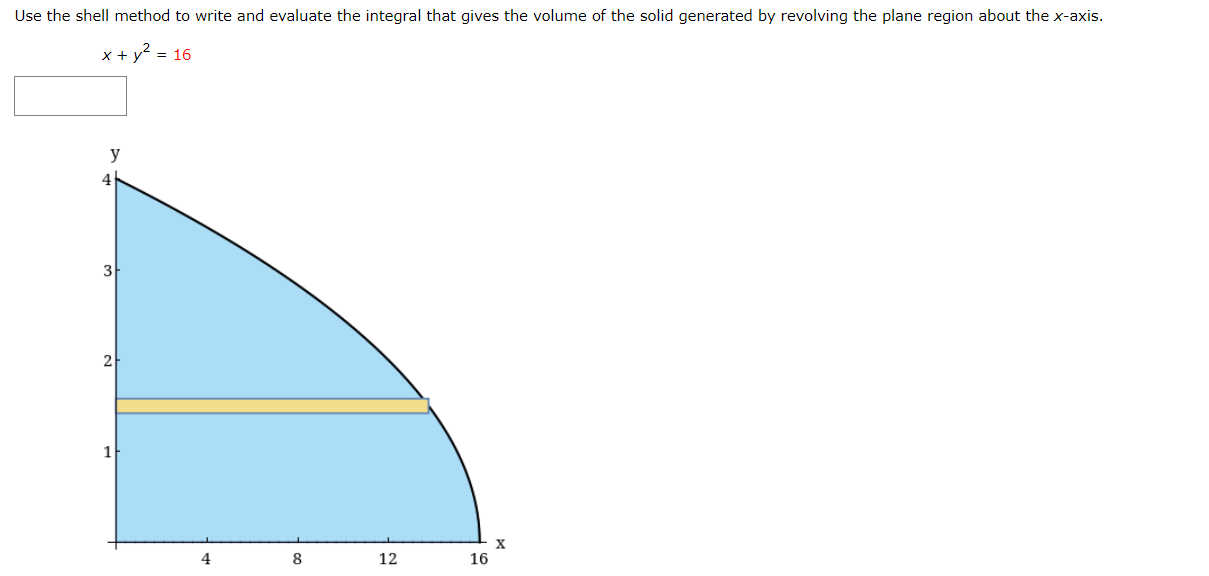



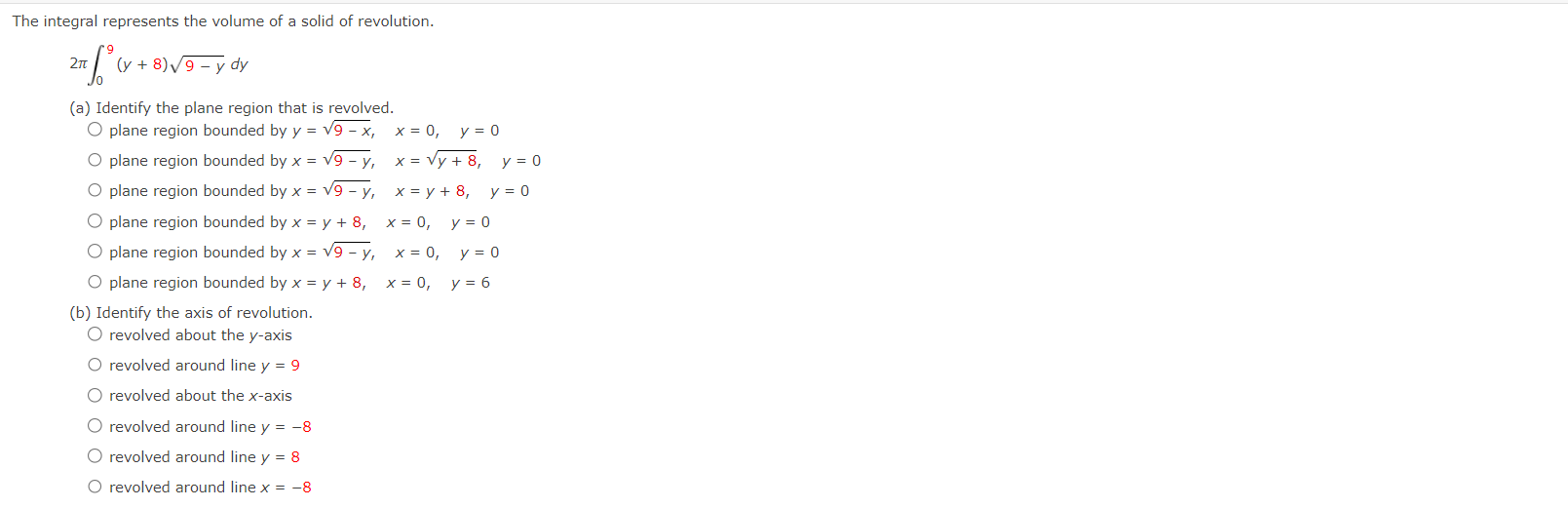

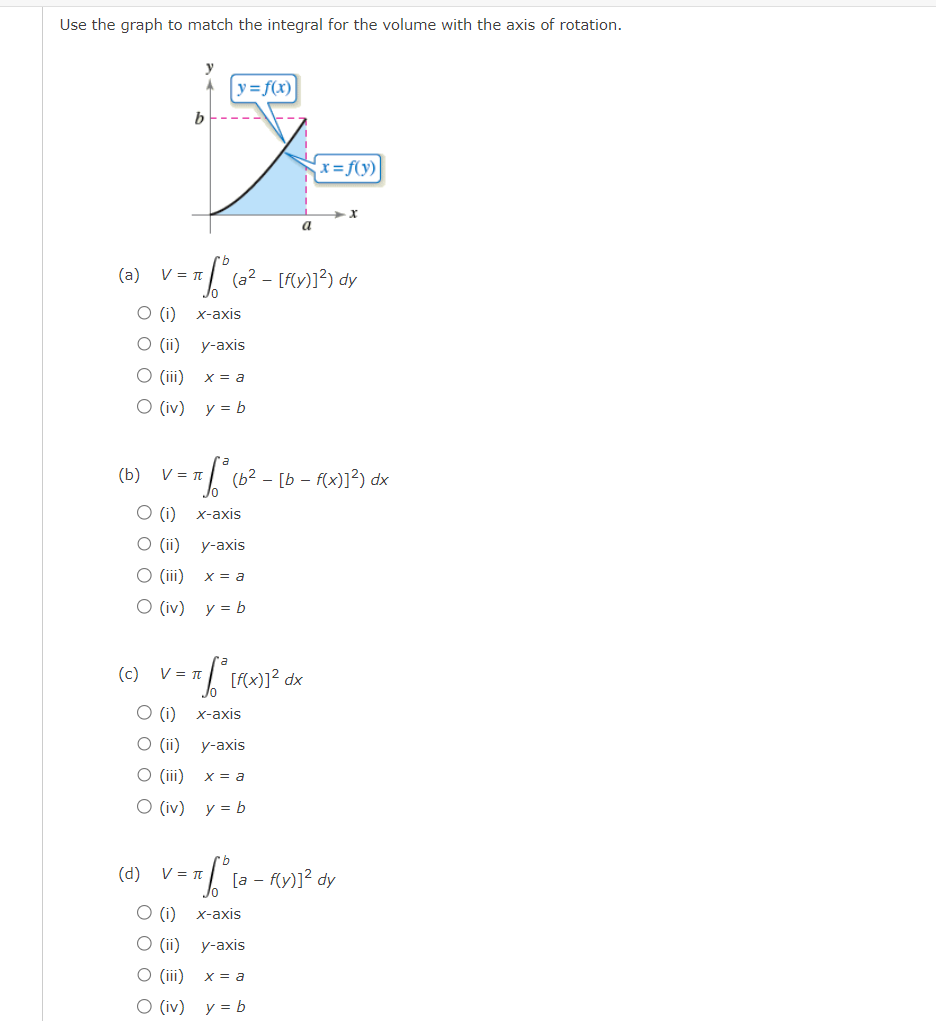
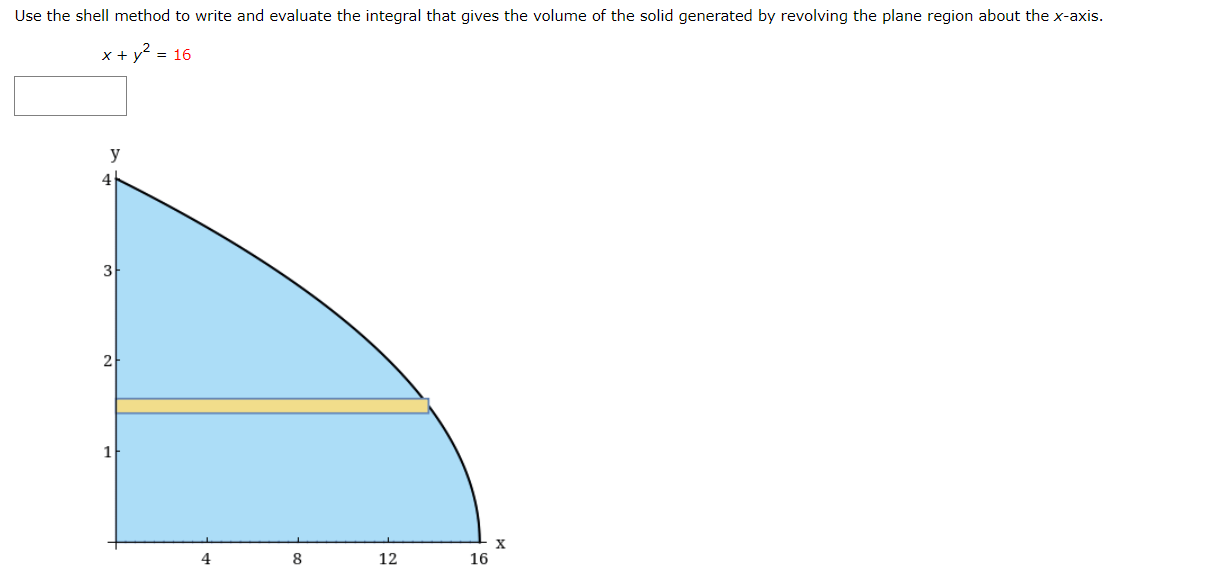
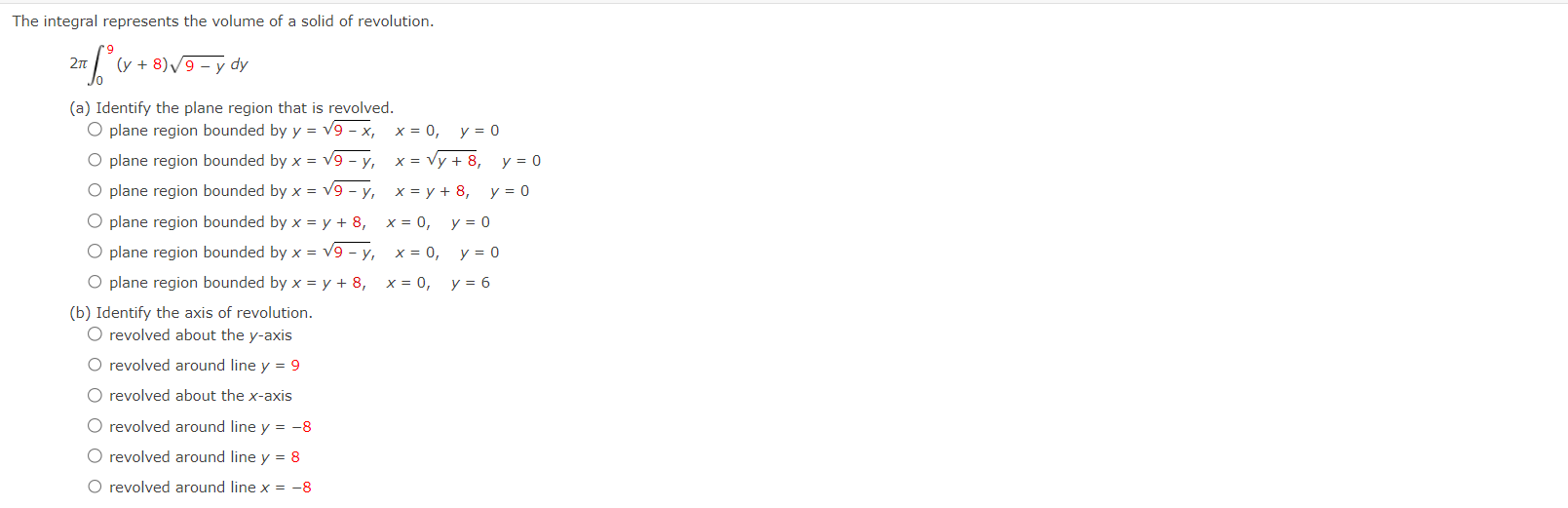
Write and evaluate the denite integral that represents the volume of the solid formed by revolving the region about the Xaxis. y:x+6 Write and evaluate the definite integral that represents the volume of the solid formed by revolving the region about the xaxis. Write and evaluate the denite integral that represents the volume of the solid formed by revolving the region about the yaxis. V:\/49x2 Find the volumes of the solids generated by revolving the regions bounded by the graphs of the equations about the given iines. V = X2 y = 6x X2 (a) the xiaxis (b) the line y = 10 Find the volume of the solid generated by revolving the specified region about the given line. R1 about X = D Use the shell method to write and evaluate the denite integral that represents the volume of the solid generated by revolving the plane region about the yaxis. y=9x Use the shell method to write and evaluate the denite integral that represents the volume of the solid generated by revolving the plane region about the xiaxis. y=1x Use the shell method to write and evaluate the definite integral that represents the volume of the solid generated by revolving the plane region about the xeaxis. 0.25 I? L] 2 0.15 01 |:| IJL Use the shell method to write and evaluate the integlal that gives the volume of the solid generated by revolving the plane region about the xaxis. x+y2=16 Use the disk method or the shell method to nd the volume of the solid generated by revolving the region bounded by the graphs of the equations about each given line. 3 KKK ii || Ii LADX (a) the rams (b) the yaxis (c) the line x : B The integral represents the volume of a solid of revolution. 3 2"] x4 dx 0 (a) Identify the plane region that is revolved. 0 plane region bounded by y = x3, 0 plane region bounded by y : x4, 0 plane region bounded by y 2 X3, 0 plane region bounded by x = ya, 0 plane region bounded by y = x4, 0 plane region bounded by y = X1!2 (b) Identify the ams of revolution. 0 revolved around the line y = 27 O revolved around the linex = 3 O revolved around the linex = 27 O revolved about the XiElXiS O revolved around the line y = 3 O revolved about the y-axis r Y=0. y=0. The integral represents the volume of a solid of revolution. 27! 09(er @de (a)1dentil"y the plane region that IS revolved. 0 plane region bounded by y = m, x 2 U, y 2 0 O plane region bounded by x = V'QT, x = m, y = O 0 plane region bounded by X = m, x = y + S, y = O 0 plane region bounded by X = y + 8, x = 0, y = D 0 plane region bounded by x : m, x : U, y : D 0 plane region bounded by x = y + 8, x = 0, y = 6 (b) Identify the awe of revolution. 0 revolved about the yeaxis O revolved around line y = 9 O revolved about the xeaxis O revolved around Ill'lE y = 78 O revolved around Ilhe y : 8 O revolved around IlneX = 78 Consider the graph of y2 : x(4 x)2 (see gure). Find the volumes of the solids that are generated when the loop of this graph is revolved about each at the following. (a) the xraxis (b) the yiaxis (c) the line x = 4
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


