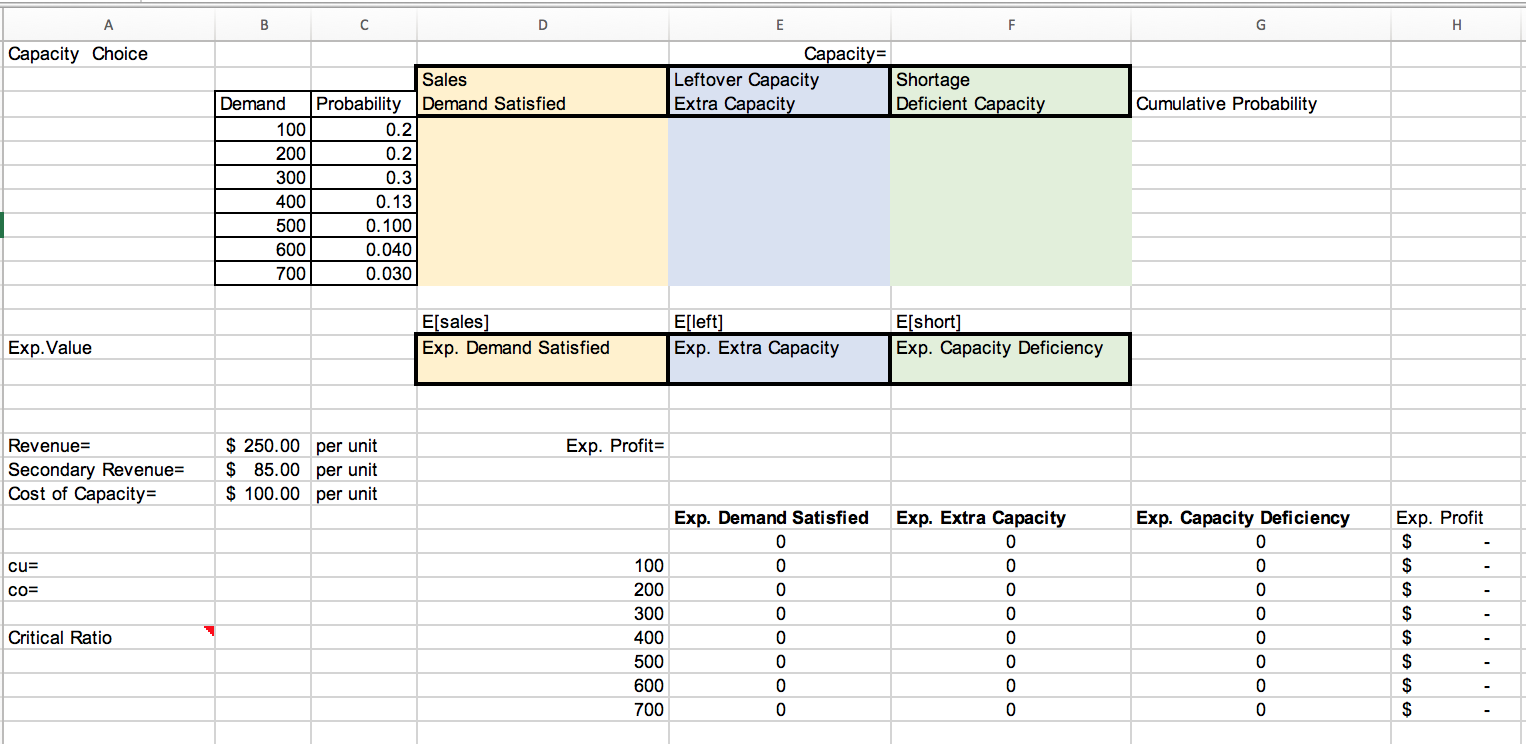
Need all the colored space to be filled and exp. profit.

Thank you!

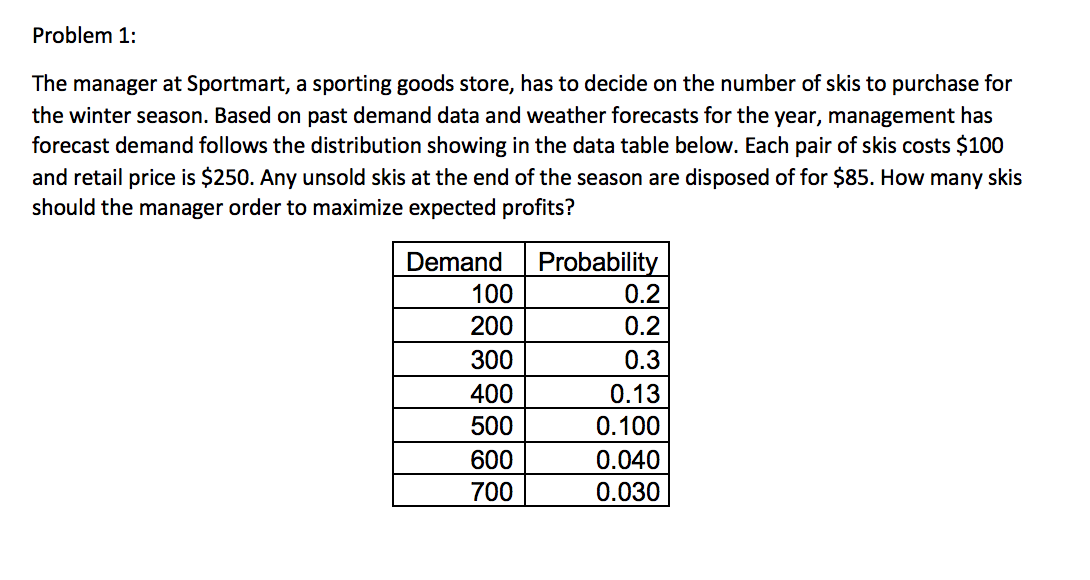
A B D E F G H Capacity Choice Capacity= Leftover Capacity Shortage Extra Capacity Deficient Capacity Cumulative Probability Sales Demand Probability Demand Satisfied 100 0.2 200 0.2 0.3 400 0.13 0.100 600 0.040 700 0.030 300 500 E[sales] Exp. Demand Satisfied E[left] Exp. Extra Capacity E[short] Exp. Capacity Deficiency Exp.Value Exp. Profit Revenue= Secondary Revenue= Cost of Capacity= $ 250.00 per unit $ 85.00 per unit $ 100.00 per unit Exp. Capacity Deficiency 0 0 cu= co= 0 Exp. Demand Satisfied 0 100 200 300 400 500 600 700 Exp. Extra Capacity 0 0 0 0 0 0 0 0 0 0 Exp. Profit $ $ $ $ $ $ $ $ Critical Ratio 0 0 0 Problem 1: The manager at Sportmart, a sporting goods store, has to decide on the number of skis to purchase for the winter season. Based on past demand data and weather forecasts for the year, management has forecast demand follows the distribution showing in the data table below. Each pair of skis costs $100 and retail price is $250. Any unsold skis at the end of the season are disposed of for $85. How many skis should the manager order to maximize expected profits? Demand 100 200 300 400 Probability 0.2 0.2 0.3 0.13 0.100 0.040 0.030 500 600 700 A B D E F G H Capacity Choice Capacity= Leftover Capacity Shortage Extra Capacity Deficient Capacity Cumulative Probability Sales Demand Probability Demand Satisfied 100 0.2 200 0.2 0.3 400 0.13 0.100 600 0.040 700 0.030 300 500 E[sales] Exp. Demand Satisfied E[left] Exp. Extra Capacity E[short] Exp. Capacity Deficiency Exp.Value Exp. Profit Revenue= Secondary Revenue= Cost of Capacity= $ 250.00 per unit $ 85.00 per unit $ 100.00 per unit Exp. Capacity Deficiency 0 0 cu= co= 0 Exp. Demand Satisfied 0 100 200 300 400 500 600 700 Exp. Extra Capacity 0 0 0 0 0 0 0 0 0 0 Exp. Profit $ $ $ $ $ $ $ $ Critical Ratio 0 0 0 Problem 1: The manager at Sportmart, a sporting goods store, has to decide on the number of skis to purchase for the winter season. Based on past demand data and weather forecasts for the year, management has forecast demand follows the distribution showing in the data table below. Each pair of skis costs $100 and retail price is $250. Any unsold skis at the end of the season are disposed of for $85. How many skis should the manager order to maximize expected profits? Demand 100 200 300 400 Probability 0.2 0.2 0.3 0.13 0.100 0.040 0.030 500 600 700