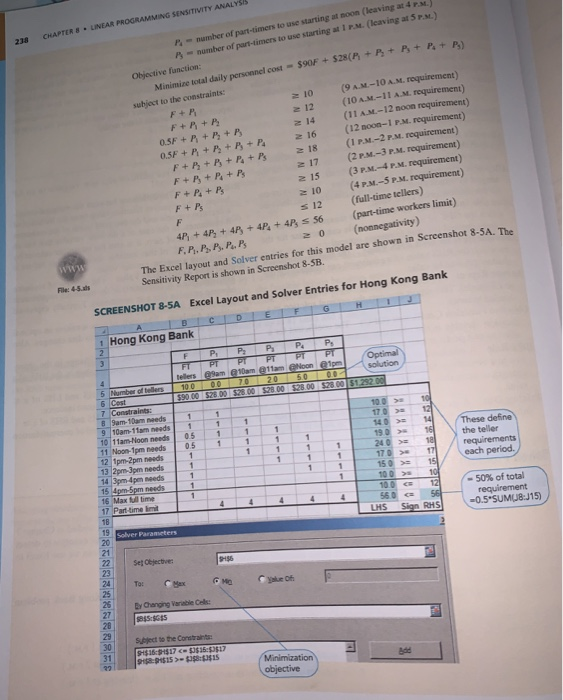
Question: need an Excel file for this ignment help asap Solved Problem Solved Problem 8-1 Consider the Hong Kong Bank of Commerce and Industry example we
need an Excel file for this ignment help asap

Solved Problem Solved Problem 8-1 Consider the Hong Kong Bank of Commerce and Industry example we first studied in Chapter 1 (section 7.5, on page 173). How can we use the Sensitivity Report for that example to detect the presence of alternate optimal solutions for an LP problem? Also, how can we use Excel to possibly identify those alternate optimal solutions? Solution For your convenience, we repeat the formulation portion of the Hong Kong Bank problem here. Define F = number of full-time tellers to use all starting at 9 A.M.) P = number of part-timers to use starting at 9 A.M. (leaving at 1 P.M.) B = number of part-timers to use starting at 10 A.M. (leaving at 2 P.M.) P. = number of part-timers to use starting at 11 A.M. (leaving at 3 P.M.) LINEAR PROGRAMMING SENSITIVITY ANALYSIS CHAPTER 8 28 R-number of part-timers to use starting at noon (leaving at 4.. leaving at 5 .) A number of part-timers to use starting at Objective function: + P + Pi Minimize total daily personnel cost - $90F + $28(A + B + B subject to the constraints: 10 (9 M-10 AM. requirement) FR F+ (10 A.M.-11 AM. requirement) +P 0.5F + + P + B (11 AM - 12 noon requirement) 0.5F +R +P + + P (12 noon-1 P. M. requirement) F+By+B+ Po+Ps (1 P.M.-2 P. M. requirement) F+B+ Pu+Ps (2 P.M.-3 P. M. requirement) F+P + P 15 (3 P.M. -4 P.M. requirement) 10 (4 P.M.-5 P.M. requirement) (full-time tellers) 47 +4, + 40 + 4P, +4P 56 (part-time workers limit) F, P, P P ,... P. 20 (nonnegativity) The Excel layout and Solver entries for this model are shown in Screenshot 8-5A. The Sensitivity Report is shown in Screenshot 8-SB. NNNNN F + PS s 12 File: 4-5. SCREENSHOT 8-5A Excel Layout and Solver Entries for Hong Kong Bank BCDEF 1 Hong Kong Bank FP, PP, PP PT These define the teller requirements cach period. OOOOOO tellers am @ am 11am Nooned 5 Number of follers1000010205000 6 Cest $28.00 59000 52.00 52800 $28.00 $28.00 $1.25200 7 Constraints: 9am-10am needs 9 10am-11am needs 10 11am-Noon needs 11 Non-1pm needs 12 1pm-2pm needs 13 2p 3pm needs 14 3pm-4pen needs 15 Apm-5pm needs 100 > 10 16 Max fillime 17 Part time in LHS Sign RHS Solver Parameters 18 alX Y YYYY Se 15 TOT 560 - SC - 50% of total requirement -0.5*SUMUJB:J15) Set Objective IMG By Changing Variable Cole: ASS Supect to the Constanta 517 $16:0517 4515 > 18:15 S Minimization objective SCREENSHOT 8-58 Solver Sensitivity Report for Hong Kong Bank Micro Excel 14. See Worksheet 145 Meta Variable Calle 5835 Number of 000 SCSS Number of teen P am0000 SOS amber of teens PT 100000 2000 SE35 Number of tellers PT 200 0 0 2000 35 Number of eers PT Choon 500 5.000.00 S655 Number of teens PT 0 0060 2300 000 Constraints Cell Allow Decrease 000 Name SHS8 Sam-10am needs SHS9 10am-11am needs SHS 10 11am-Noon needs SHS11 Noon-1pm needs SH$ 12 tpm-2pm needs SH$13 2pm-3pm needs SHS 14 3pm-4pm needs SHS15 4pm-5pm needs SH$ 16 Max full time SHS17 Part-time limit Final Shadow Constraint how Value Police RH Side Increase 10 00 17.00 1200 14 00 60.00 1400 19.00 1600 24 00 17.00 15 00 3 00 1E430 15-30 8888888 08 10.00 888888 8818181818218 3.00 0.00 10.00 56 001 Screenshot 8-SA reveals that the optimal solution is to employ 10 full-time tellers, 7 part- time tellers at 10 A.M., 2 part time tellers at 11 AM, and cost of $1,292 per day. part-time tellers at noon, for a total In Screenshot 8-5B, the shadow price of -$8 for the part-time limit of 56 hours indicates that each additional hour (over the 56-hour limit) that part-time tellers are allowed to work will allow the bank to reduce costs by $8. This shadow price is valid for a limit of 60 more hours (i.e., up to 116 hours). Examining the Allowable Increase and Allowable Decrcase columns for the OFCs, we see that there are several values of zero in these columns. This indicates that there are alternate optimal solutions to this problem. Likewise, consider the reduced cost for variables (part-timers starting at 9 A.M.) and P (part-timers starting at 1 P.M.). These are zero, even though these variables have values of zero (their lower limit). This implies that, for example, it is possible to force P (or Ps) to have a nonzero value at optimality and not affect the total cost in any way. This is another indication of the presence of alternate optimal solutions to this problem. How can we identify these optimal solutions by using Excel's Solver? There are at least a couple ways of doing so. First, simply rearranging the order in which the variables and/or constraints are included in the Excel layout may make Solver identify an alternate optimal solution. That is, we can just swap the order in which some of the rows andor columns are included in the model. There is, however, no guarantee that this approach will always identify an alternate optimal solution. can force Excel to identify mate optimal solutions. The second approach, which will definitely find an alternate optimal solution (if one exists), is as follows. From the preceding discussion, we know that variable (which cur rently has a zero value) can have a nonzero value at an optimal solution. To force this to happen, we include the current objective function as a constraint, as follows: $90F + $28(P) + B + B + PA+ Ps) = $1,292 n optimal solution) P. We can ong Kong Bank, as This will force the new solution to have the same optimal cost (1.e., it is also an optimal Then, the new objective for the model would be Max P. Note that this will find a solution that costs $1,292 but has a nonzero value for PW repeat the same approach with the variable P to find yet another optimal solution. Using these approaches, we can identify two alternate solutions for Hong Kong B. follows: 1. 10 full-time tellers, 6 part-time tellers at 9 A.M., 1 part-time teller at 10 A.M., 2 part-time tellers at 11 A.m., and 5 part-time tellers at noon. 2. 10 full-time tellers, 6 part-time tellers at 9 A.M., 1 part-time teller at 10 A.M., 2 part-time tellers at 11 A.M., 2 part-time tellers at noon, and 3 part-time tellers at 10 A.M. The cost of each of these employment policies is also $1,292. Solved Problem Solved Problem 8-1 Consider the Hong Kong Bank of Commerce and Industry example we first studied in Chapter 1 (section 7.5, on page 173). How can we use the Sensitivity Report for that example to detect the presence of alternate optimal solutions for an LP problem? Also, how can we use Excel to possibly identify those alternate optimal solutions? Solution For your convenience, we repeat the formulation portion of the Hong Kong Bank problem here. Define F = number of full-time tellers to use all starting at 9 A.M.) P = number of part-timers to use starting at 9 A.M. (leaving at 1 P.M.) B = number of part-timers to use starting at 10 A.M. (leaving at 2 P.M.) P. = number of part-timers to use starting at 11 A.M. (leaving at 3 P.M.) LINEAR PROGRAMMING SENSITIVITY ANALYSIS CHAPTER 8 28 R-number of part-timers to use starting at noon (leaving at 4.. leaving at 5 .) A number of part-timers to use starting at Objective function: + P + Pi Minimize total daily personnel cost - $90F + $28(A + B + B subject to the constraints: 10 (9 M-10 AM. requirement) FR F+ (10 A.M.-11 AM. requirement) +P 0.5F + + P + B (11 AM - 12 noon requirement) 0.5F +R +P + + P (12 noon-1 P. M. requirement) F+By+B+ Po+Ps (1 P.M.-2 P. M. requirement) F+B+ Pu+Ps (2 P.M.-3 P. M. requirement) F+P + P 15 (3 P.M. -4 P.M. requirement) 10 (4 P.M.-5 P.M. requirement) (full-time tellers) 47 +4, + 40 + 4P, +4P 56 (part-time workers limit) F, P, P P ,... P. 20 (nonnegativity) The Excel layout and Solver entries for this model are shown in Screenshot 8-5A. The Sensitivity Report is shown in Screenshot 8-SB. NNNNN F + PS s 12 File: 4-5. SCREENSHOT 8-5A Excel Layout and Solver Entries for Hong Kong Bank BCDEF 1 Hong Kong Bank FP, PP, PP PT These define the teller requirements cach period. OOOOOO tellers am @ am 11am Nooned 5 Number of follers1000010205000 6 Cest $28.00 59000 52.00 52800 $28.00 $28.00 $1.25200 7 Constraints: 9am-10am needs 9 10am-11am needs 10 11am-Noon needs 11 Non-1pm needs 12 1pm-2pm needs 13 2p 3pm needs 14 3pm-4pen needs 15 Apm-5pm needs 100 > 10 16 Max fillime 17 Part time in LHS Sign RHS Solver Parameters 18 alX Y YYYY Se 15 TOT 560 - SC - 50% of total requirement -0.5*SUMUJB:J15) Set Objective IMG By Changing Variable Cole: ASS Supect to the Constanta 517 $16:0517 4515 > 18:15 S Minimization objective SCREENSHOT 8-58 Solver Sensitivity Report for Hong Kong Bank Micro Excel 14. See Worksheet 145 Meta Variable Calle 5835 Number of 000 SCSS Number of teen P am0000 SOS amber of teens PT 100000 2000 SE35 Number of tellers PT 200 0 0 2000 35 Number of eers PT Choon 500 5.000.00 S655 Number of teens PT 0 0060 2300 000 Constraints Cell Allow Decrease 000 Name SHS8 Sam-10am needs SHS9 10am-11am needs SHS 10 11am-Noon needs SHS11 Noon-1pm needs SH$ 12 tpm-2pm needs SH$13 2pm-3pm needs SHS 14 3pm-4pm needs SHS15 4pm-5pm needs SH$ 16 Max full time SHS17 Part-time limit Final Shadow Constraint how Value Police RH Side Increase 10 00 17.00 1200 14 00 60.00 1400 19.00 1600 24 00 17.00 15 00 3 00 1E430 15-30 8888888 08 10.00 888888 8818181818218 3.00 0.00 10.00 56 001 Screenshot 8-SA reveals that the optimal solution is to employ 10 full-time tellers, 7 part- time tellers at 10 A.M., 2 part time tellers at 11 AM, and cost of $1,292 per day. part-time tellers at noon, for a total In Screenshot 8-5B, the shadow price of -$8 for the part-time limit of 56 hours indicates that each additional hour (over the 56-hour limit) that part-time tellers are allowed to work will allow the bank to reduce costs by $8. This shadow price is valid for a limit of 60 more hours (i.e., up to 116 hours). Examining the Allowable Increase and Allowable Decrcase columns for the OFCs, we see that there are several values of zero in these columns. This indicates that there are alternate optimal solutions to this problem. Likewise, consider the reduced cost for variables (part-timers starting at 9 A.M.) and P (part-timers starting at 1 P.M.). These are zero, even though these variables have values of zero (their lower limit). This implies that, for example, it is possible to force P (or Ps) to have a nonzero value at optimality and not affect the total cost in any way. This is another indication of the presence of alternate optimal solutions to this problem. How can we identify these optimal solutions by using Excel's Solver? There are at least a couple ways of doing so. First, simply rearranging the order in which the variables and/or constraints are included in the Excel layout may make Solver identify an alternate optimal solution. That is, we can just swap the order in which some of the rows andor columns are included in the model. There is, however, no guarantee that this approach will always identify an alternate optimal solution. can force Excel to identify mate optimal solutions. The second approach, which will definitely find an alternate optimal solution (if one exists), is as follows. From the preceding discussion, we know that variable (which cur rently has a zero value) can have a nonzero value at an optimal solution. To force this to happen, we include the current objective function as a constraint, as follows: $90F + $28(P) + B + B + PA+ Ps) = $1,292 n optimal solution) P. We can ong Kong Bank, as This will force the new solution to have the same optimal cost (1.e., it is also an optimal Then, the new objective for the model would be Max P. Note that this will find a solution that costs $1,292 but has a nonzero value for PW repeat the same approach with the variable P to find yet another optimal solution. Using these approaches, we can identify two alternate solutions for Hong Kong B. follows: 1. 10 full-time tellers, 6 part-time tellers at 9 A.M., 1 part-time teller at 10 A.M., 2 part-time tellers at 11 A.m., and 5 part-time tellers at noon. 2. 10 full-time tellers, 6 part-time tellers at 9 A.M., 1 part-time teller at 10 A.M., 2 part-time tellers at 11 A.M., 2 part-time tellers at noon, and 3 part-time tellers at 10 A.M. The cost of each of these employment policies is also $1,292