need correct answer in haskell

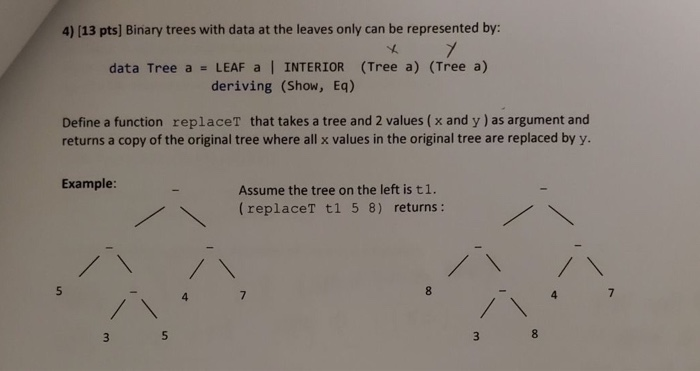
4) (13 pts) Binary trees with data at the leaves only can be represented by: XY data Tree a = LEAF a | INTERIOR (Tree a) (Tree a) deriving (Show, Eq) Define a function replaces that takes a tree and 2 values (x and y) as argument and returns a copy of the original tree where all x values in the original tree are replaced by y. Example: Assume the tree on the left is ti. (replacet ti 5 8) returns: 3 5 5) (20 pts] We want to define a Haskell function (apply opil) that applies op to every element in the input list (iL) and returns a list of tuples where the first element in each tuple is a value from il and the second value is the result of op applied to that value. For example, apply (\x -> x*x) [3,5,7,6] returns [(3,9),(5,25),(7,49), (6,36)] apply length ["one", "two", "three") returns [("one",3),("two",3), ("three", 5)] (a) (10 pts) Give a recursive definition of the apply function. OR apply k l = [] Il Check it list is empty apply L (x,(x:xs) - apply op Y:(xs) -6 Il call apply agu and argend op into y and all to list imput list is not necessarily a list a tuples (b) (10 pts) Re-define the apply function using map function. Your solution should not use explicit recursion. You may need to define additional non-recursive helper function(s). map a aply Yil - Map Cop (x,y)) il 4) (13 pts) Binary trees with data at the leaves only can be represented by: XY data Tree a = LEAF a | INTERIOR (Tree a) (Tree a) deriving (Show, Eq) Define a function replaces that takes a tree and 2 values (x and y) as argument and returns a copy of the original tree where all x values in the original tree are replaced by y. Example: Assume the tree on the left is ti. (replacet ti 5 8) returns: 3 5 5) (20 pts] We want to define a Haskell function (apply opil) that applies op to every element in the input list (iL) and returns a list of tuples where the first element in each tuple is a value from il and the second value is the result of op applied to that value. For example, apply (\x -> x*x) [3,5,7,6] returns [(3,9),(5,25),(7,49), (6,36)] apply length ["one", "two", "three") returns [("one",3),("two",3), ("three", 5)] (a) (10 pts) Give a recursive definition of the apply function. OR apply k l = [] Il Check it list is empty apply L (x,(x:xs) - apply op Y:(xs) -6 Il call apply agu and argend op into y and all to list imput list is not necessarily a list a tuples (b) (10 pts) Re-define the apply function using map function. Your solution should not use explicit recursion. You may need to define additional non-recursive helper function(s). map a aply Yil - Map Cop (x,y)) il