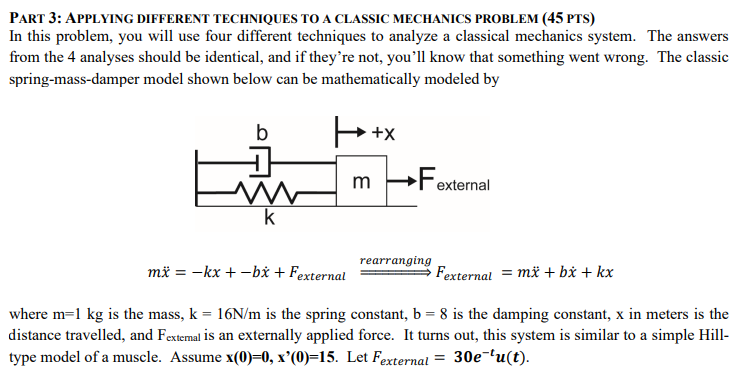
PART 3: APPLYING DIFFERENT TECHNIQUES TO A CLASSIC MECHANICS PROBLEM (45 PTS) In this problem, you will use four different techniques to analyze a classical mechanics system. The answers from the 4 analyses should be identical, and if they're not, you'll know that something went wrong. The classic spring-mass-damper model shown below can be mathematically modeled by b k X+H m Fexternal rearranging mx = kx + -bx + Fexternal Fexternal = mx + bx + kx where m=1 kg is the mass, k = 16N/m is the spring constant, b = 8 is the damping constant, x in meters is the distance travelled, and Fexternal is an externally applied force. It turns out, this system is similar to a simple Hill- type model of a muscle. Assume x(0)=0, x'(0)=15. Let Fexternal = 30e-u(t). 4. Analyze the system using Discrete Fourier Transforms (12 pts) Now you're going to use discrete Fourier transforms (fft) to analyze the system. To do this, you'll want to: 1. Create a vector f(t) and h(t). 2. Use a fast Fourier transform to get F() and H(o) 3. Calculate X() 4. Use the inverse fast Fourier transform to get x(t) In the lower right of a 2x2 subplot, plot x(t). As with the previous plot, you should notice that x(t) is not the system response for the same reason that it wasn't before. Add a second line to your plot after you add in the correction. Remember: labels, units, legends, titles, and distinct lines.