need help on circled question

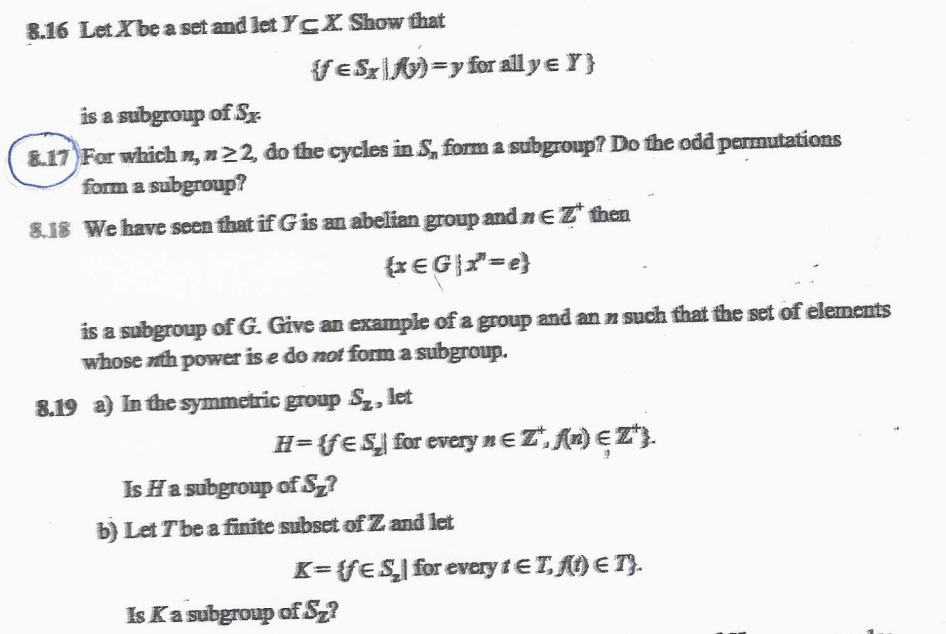
8.16 Let Xbe a set and let ) C X. Show that {f ESx/(y)=y for all yer} is a subgroup of Sx. 8.17 For which n, # 2 2, do the cycles in S, form a subgroup? Do the odd permutations form a subgroup? 8.18 We have seen that if G is an abelian group and ne Z* then (x EGx=e) is a subgroup of G. Give an example of a group and an in such that the set of elements whose wth power is e do not form a subgroup. 8.19 a) In the symmetric group S,, let H= {f ES,| for every ne Z*, An) EZ'). Is H a subgroup of Sz? b) Let T'be a finite subset of Z and let K= (fES | for every t E I, ((() ET). Is K a subgroup of Sz