Need help;

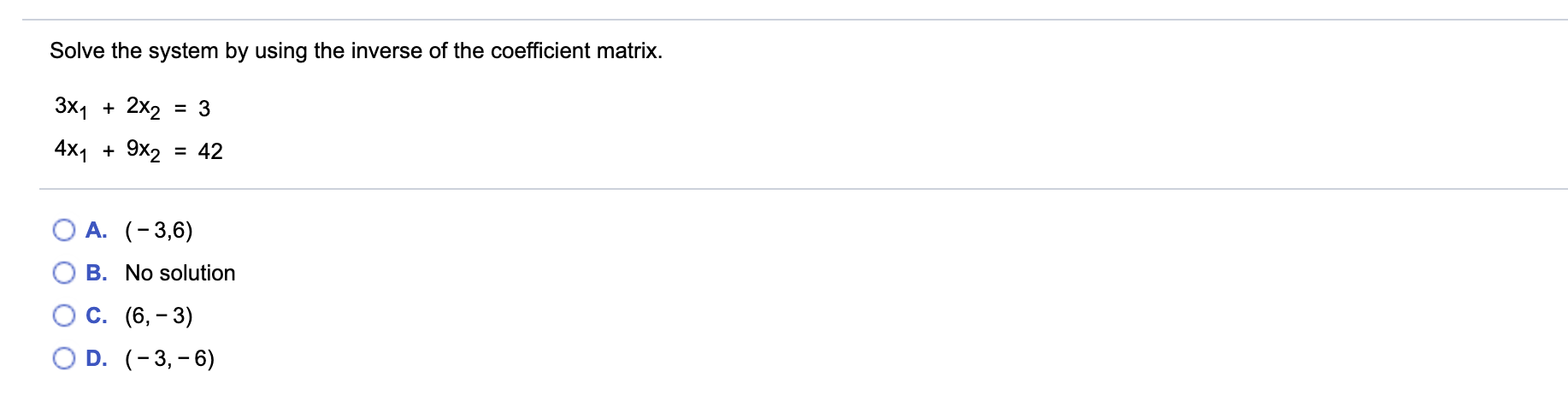
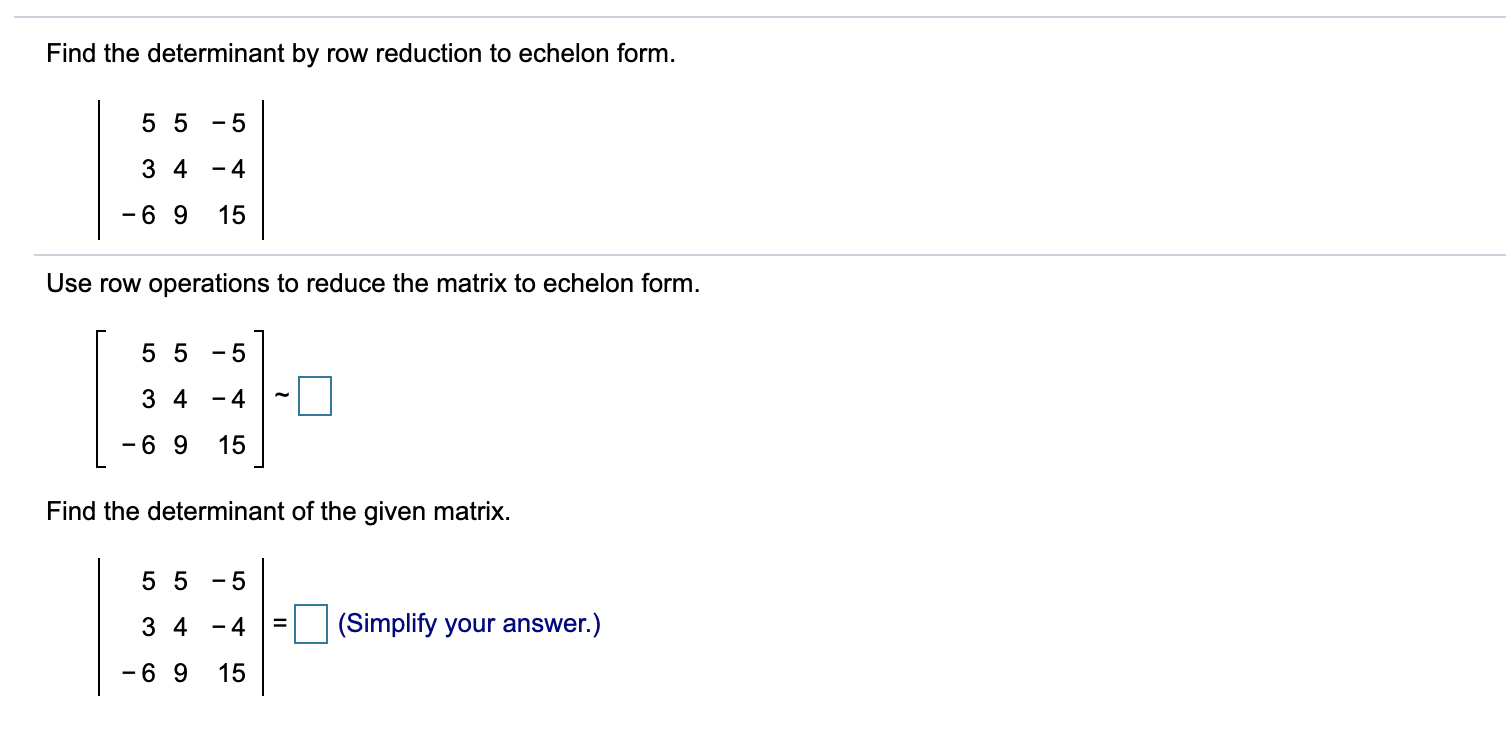
Solve the system by using the inverse of the coefficient matrix. 3x1 + 2x2 = 3 4X1 + 9X2 = 42 O A. (-3,6) O B. No solution O C. (6, -3) O D. (-3, -6)Find the determinant by row reduction to echelon form. 5 5 - 5 3 4 -4 -6 9 15 Use row operations to reduce the matrix to echelon form. 5 5 -5 3 4 -4 9 15 Find the determinant of the given matrix. 5 5 - 5 3 4 -4 (Simplify your answer.) -6 9 15Compute the adjugate of the given matrix, and then use the Inverse Formula to give the inverse of the matrix. 475 A= 101 321 The adjugate of the given matrix is adj A = _ ' |_| The inverse of the given matrix isA'1 = _| ' |_| (Simplify your answers.) Use Cramer's rule to compute the solution of the system. What is the solution of the system? 5 x1 + X2 = 17 X1 = X2 = 4X1 + 7X2 = 26 (Type integers or simplified fractions.)