need help to solve please see attached

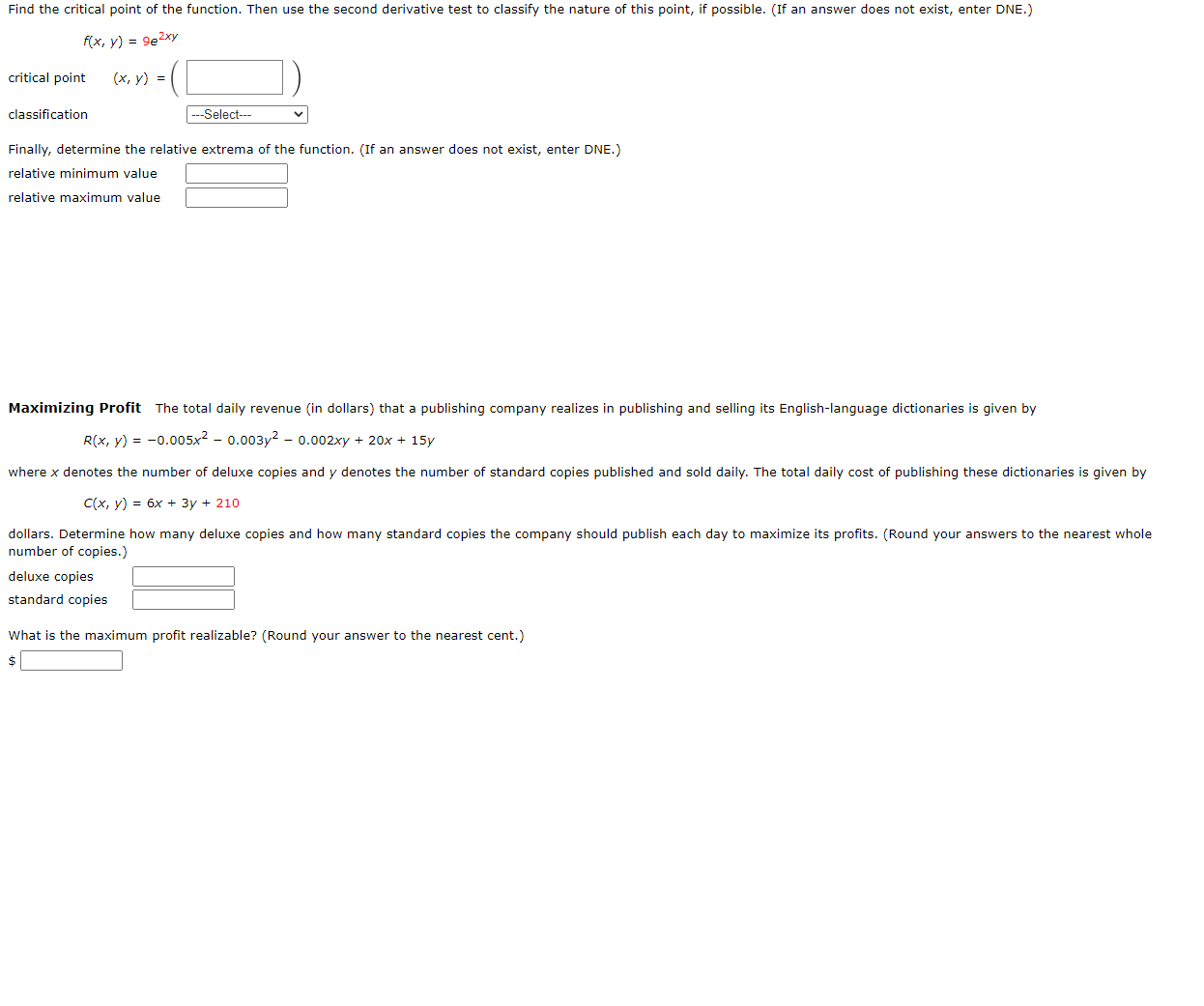
Find the critical point of the function. Then use the second derivative test to classify the nature of this point, if possible. [If an answer does not exist, enter DNE.) X. y) = 992'? critical point (x, y} = ( ) classification -Seled V Finally, determine the relative extrema of the function. (If an answer does not exist, enter DNE.) relative minimum value relative maximum value Maximizing Profit The total daily revenue (in dollars} that a publishing company realizes in publishing and selling its English-language dictionaries is given by R(x, y) = o.005x2 0.0031,:2 0.130ny + 20): + 15y wherex denotes the number of deluxe copies and 5! denotes the number of standard copies published and sold daily. The total daily cost of publishing these dictionaries is given by C(x, y) = 6x + By + 210 dollars. Determine how many deluxe copies and how many standard copies the company should publish each day to maximize its prots. [Round your answers to the nearest whole number of copies.) standard copies :| What is the maximum prot realizable? [Round your answer to the nearest cent.) $|:|