Need help utilizing Python 3 to solve these problems. Thank you.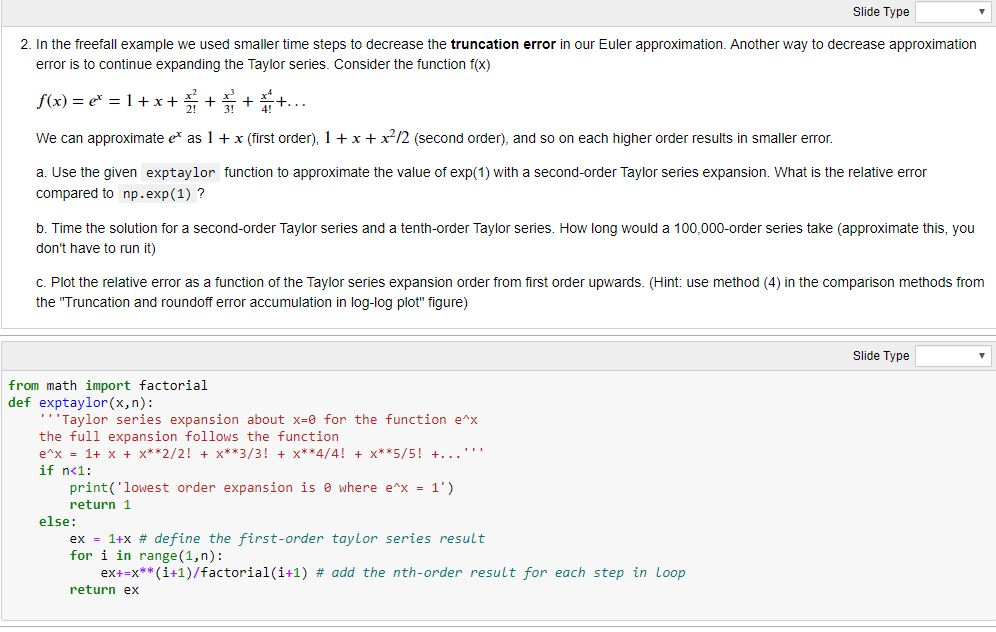

Slide Type 2. In the freefall example we used smaller time steps to decrease the truncation error in our Euler approximation. Another way to decrease approximation error is to continue expanding the Taylor series. Consider the function f(x) f(x) = et = 1+x+*+ +*+... We can approximate et as 1 + x (first order), 1 + x +x+/2 (second order), and so on each higher order results in smaller error. a. Use the given exptaylor function to approximate the value of exp(1) with a second-order Taylor series expansion. What is the relative error compared to np.exp(1) ? b. Time the solution for a second-order Taylor series and a tenth-order Taylor series. How long would a 100,000-order series take (approximate this, you don't have to run it) C. Plot the relative error as a function of the Taylor series expansion order from first order upwards. (Hint: use method (4) in the comparison methods from the "Truncation and roundoff error accumulation in log-log plot" figure) Slide Type from math import factorial def exptaylor(x,n): "Taylor series expansion about x=0 for the function ex the full expansion follows the function e^x = 1+ x + ***2/2! + x**3/3! + ***4/4! + ***5/5! +...'' if n