Need help with question 1 (a,b,c)

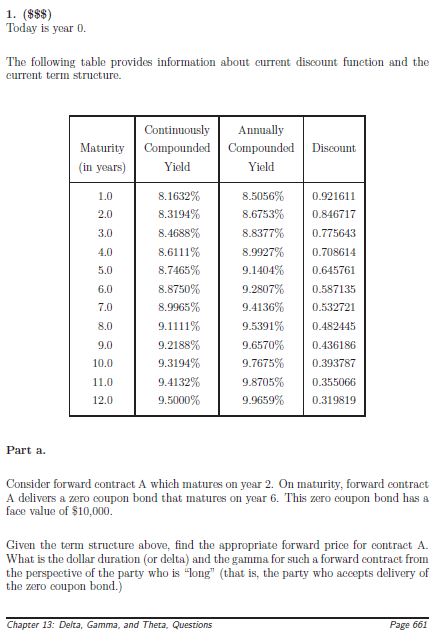
1. ($$) Today is year 0 . The following table provides information about current discount funetion and the eurrent term structure. Part a. Consider forward contract A which matures on year 2. On maturity, forward contract A delivers a zero coupon bond that matures on year 6 . This zero coupon bond has a face value of $10,000. Given the term structure above, find the appropriate forward price for contract A. What is the dollar duration (or delta) and the gamma for such a forward contract from the perspective of the party who is "long" (that is, the party who accepts delivery of the zero coupon bond.) Consider a forward contract B which matures on year 4. On maturity, forward contract B delivers a zero coupon bond that matures on year 6 . This zero coupon bond has a face value of $10,000. Given the above term structure, the appropriate forward price for contract B is $8285.68, the dollar duration (or delta) of contract B is 117.4271 , and the gamma of contract B is 11.7427. Now find a combination of forward contracts A and B such that the dollar duration (or the delta) is zero Part. The net equity for your eurrent balance sheet is $39,576.89. The dollar duration (or delta) and gamma for this net equity under your current balance sheet is 1187.31 and -106.47, respectively. You would like your net equity to behave as if you had all your wealth in a three year zero coupon bond. Using Forward Contracts A and B, find the proper number of forward contracts to achieve a delta and a gamma for your net equity that is appropriate if you want your net equity to behave as if it were invested in three year zero coupon bonds. You should be able to find the solution to this question solving only one equation and one unknown. Only partial credit will be given if your solution involves more work than this. 1. ($$) Today is year 0 . The following table provides information about current discount funetion and the eurrent term structure. Part a. Consider forward contract A which matures on year 2. On maturity, forward contract A delivers a zero coupon bond that matures on year 6 . This zero coupon bond has a face value of $10,000. Given the term structure above, find the appropriate forward price for contract A. What is the dollar duration (or delta) and the gamma for such a forward contract from the perspective of the party who is "long" (that is, the party who accepts delivery of the zero coupon bond.) Consider a forward contract B which matures on year 4. On maturity, forward contract B delivers a zero coupon bond that matures on year 6 . This zero coupon bond has a face value of $10,000. Given the above term structure, the appropriate forward price for contract B is $8285.68, the dollar duration (or delta) of contract B is 117.4271 , and the gamma of contract B is 11.7427. Now find a combination of forward contracts A and B such that the dollar duration (or the delta) is zero Part. The net equity for your eurrent balance sheet is $39,576.89. The dollar duration (or delta) and gamma for this net equity under your current balance sheet is 1187.31 and -106.47, respectively. You would like your net equity to behave as if you had all your wealth in a three year zero coupon bond. Using Forward Contracts A and B, find the proper number of forward contracts to achieve a delta and a gamma for your net equity that is appropriate if you want your net equity to behave as if it were invested in three year zero coupon bonds. You should be able to find the solution to this question solving only one equation and one unknown. Only partial credit will be given if your solution involves more work than this