need help with the following 3 problems

Problem 1)

A relation R on the set of integers is given as follows: R = {(x, y) such that x ? 3y ? 1}. Answer the following questions, and explain your answers.

(a) Is R reflexive?

(b) Is R symmetric?

(c) Is R antisymmetric?

(d) Is R transitive?

Problem 2)

A relation R on the set of real numbers is given as follows: R = {(x, y) such that y = xz for some real number z > 0}. Determine if R is an equivalence relation; if so, find the corresponding partition of the real numbers by specifying the equivalence classes. 1

Problem 3)

Prove that for all positive integers n,

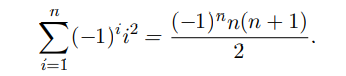
\f