Need help with these 2 question asap...

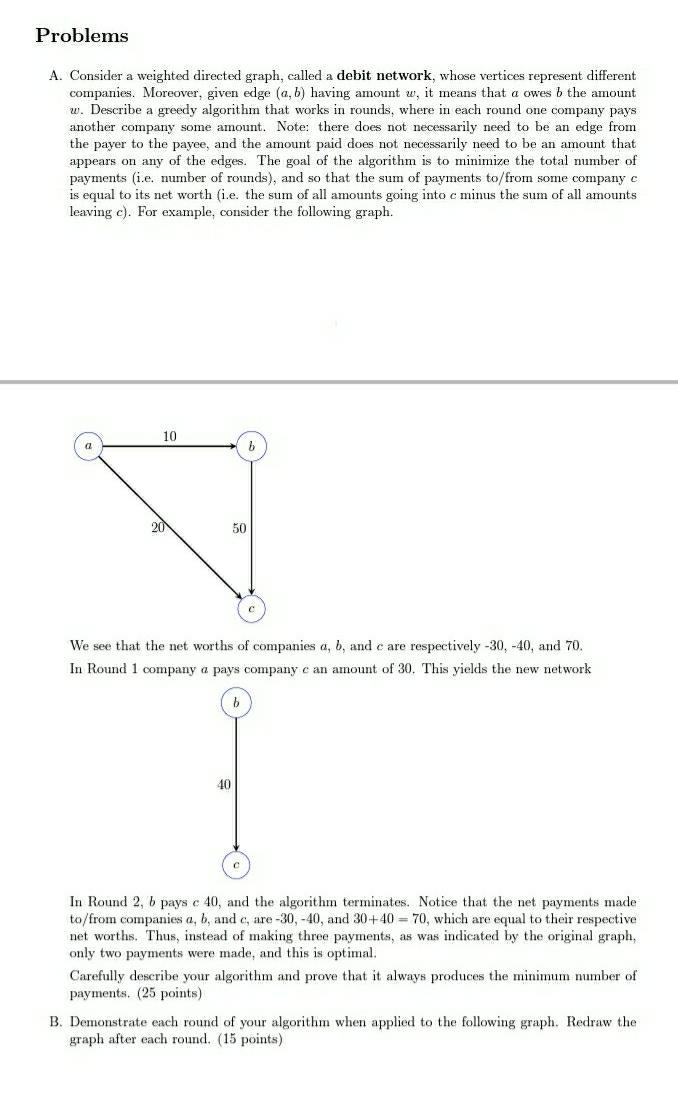
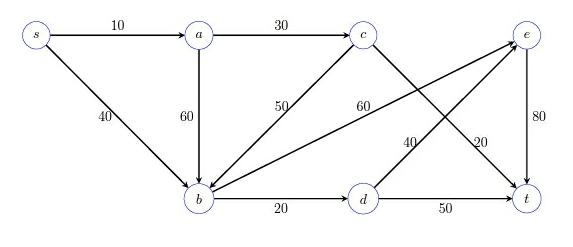
Problems A. Consider a weighted directed graph, called a debit network, whose vertices represent different companies. Moreover, given edge (a,b) having amount w, it means that a owes b the amount w. Describe a greedy algorithm that works in rounds, where in each round one company pays another company some amount. Note: there does not necessarily need to be an edge from the payer to the payee, and the amount paid does not necessarily need to be an amount that appears on any of the edges. The goal of the algorithm is to minimize the total number of payments (ie. number of rounds), and so that the sum of payments to/from some company c is equal to its net worth (i.e. the sum of all amounts going into c minus the sum of all amounts leaving c). For example, consider the following graph. 10 20 50 We see that the net worths of companies a, b, and c are respectively -30, -40, and 70. In Round 1 company a pays company c an amount of 30. This yields the new network 40 In Round 2, b pays c 40, and the algorithm terminates. Notice that the net payments made to/from companies a, b, and c, are -30,-40, and 30+40 = 70, which are equal to their respective net worths. Thus, instead of making three payments, as was indicated by the original graph, only two payments were made, and this is optimal. Carefully describe your algorithm and prove that it always produces the minimum number of payments. (25 points) B. Demonstrate each round of your algorithm when applied to the following graph. Redraw the graph after each round. (15 points) 10 30 5 a 50 60 60 80 40 20 d + 20 50 Problems A. Consider a weighted directed graph, called a debit network, whose vertices represent different companies. Moreover, given edge (a,b) having amount w, it means that a owes b the amount w. Describe a greedy algorithm that works in rounds, where in each round one company pays another company some amount. Note: there does not necessarily need to be an edge from the payer to the payee, and the amount paid does not necessarily need to be an amount that appears on any of the edges. The goal of the algorithm is to minimize the total number of payments (ie. number of rounds), and so that the sum of payments to/from some company c is equal to its net worth (i.e. the sum of all amounts going into c minus the sum of all amounts leaving c). For example, consider the following graph. 10 20 50 We see that the net worths of companies a, b, and c are respectively -30, -40, and 70. In Round 1 company a pays company c an amount of 30. This yields the new network 40 In Round 2, b pays c 40, and the algorithm terminates. Notice that the net payments made to/from companies a, b, and c, are -30,-40, and 30+40 = 70, which are equal to their respective net worths. Thus, instead of making three payments, as was indicated by the original graph, only two payments were made, and this is optimal. Carefully describe your algorithm and prove that it always produces the minimum number of payments. (25 points) B. Demonstrate each round of your algorithm when applied to the following graph. Redraw the graph after each round. (15 points) 10 30 5 a 50 60 60 80 40 20 d + 20 50