need help with these linear algebra questions

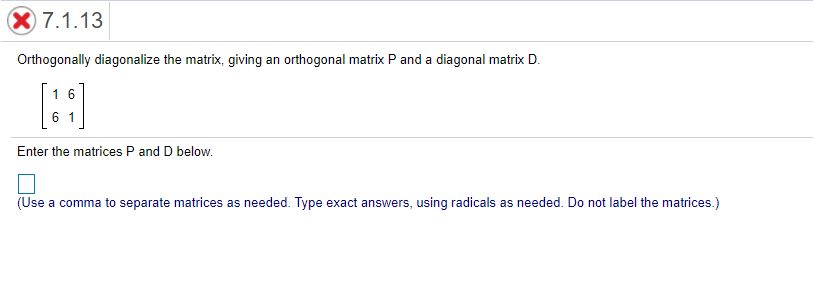
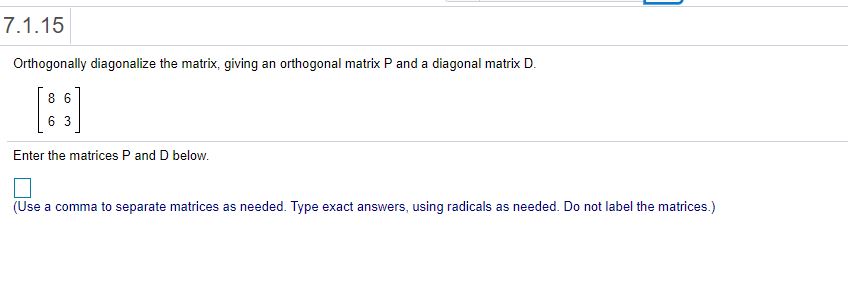
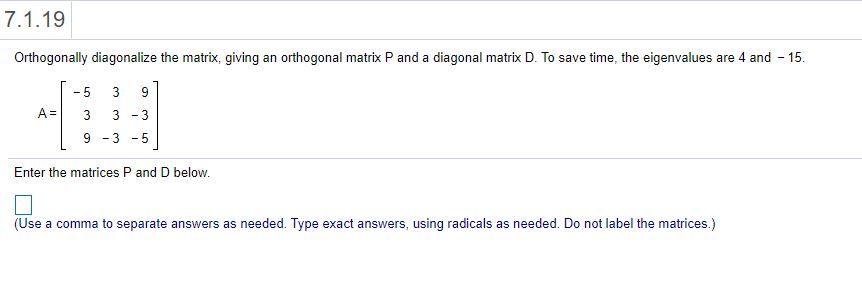
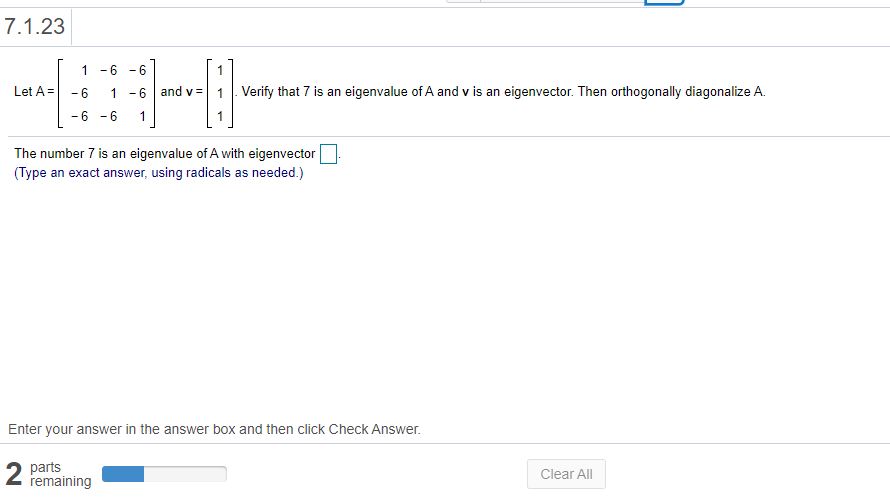
7.1.5' 9 3 I] Determine ifthe matrix 3 3 ? is symmetric. D-i'? Select the correct choice below and. ifnecessary, ll in the answer box within your choice. (Simplify your answer.) 0 - The matrix is not symmetric because it is not equal to its inverse, which is |:. O B- The matrix is not symmetn'c because it is not equai to its transpose, which is O C' The matrix is symmetric because it is equal to the negative of its transpose. which is |:. O D- The math): is not symmetric because it is not equal to the negative oiits transpose, which is O E- The matrix is symmetric because it is equal to its inverse, which is O F- The matrix is symmetn'c because it is equal to its transpose, which is j. 7.1.13' Orthogonally diagonalize the matrix, giving an orthogcnal matrix P and a diagonal matrix D. iii Enter die matrices P and D below. (Use a comma to separate matrices as needed. Type exad answers, using radicals as needed. Do not label the matrices.) 7.1.15 Orlhogonally diagonalize the matrix, giving an orlhogonal matrix F' and a diagonal matrix D. [33] Enter the matrices P and D below. (Use a comma to separate matrices as needed. Type axed answers, using radicals as needed. Do not label the matrices.) 7.1.19 Orthogonally diagonalize the matrix, giving an orthogonal matrix P and a diagonal matrix D. To save time, the eigenvalues are 4 and 15. 5 3 9 A: 3 3 3 9 -3 -5 Enter the matrices P and D bebw. (Use a comma to separate answers as needed. Type exact answers, using radicals as needed. Do not label the matrices.) 7.1.23 1 -6 -6 Let A = -6 1 -6|and v = Verify that 7 is an eigenvalue of A and v is an eigenvector. Then orthogonally diagonalize A. -6 -6 The number 7 is an eigenvalue of A with eigenvector (Type an exact answer, using radicals as needed.) Enter your answer in the answer box and then click Check Answer. 2 parts remaining Clear All