Need help with these plz

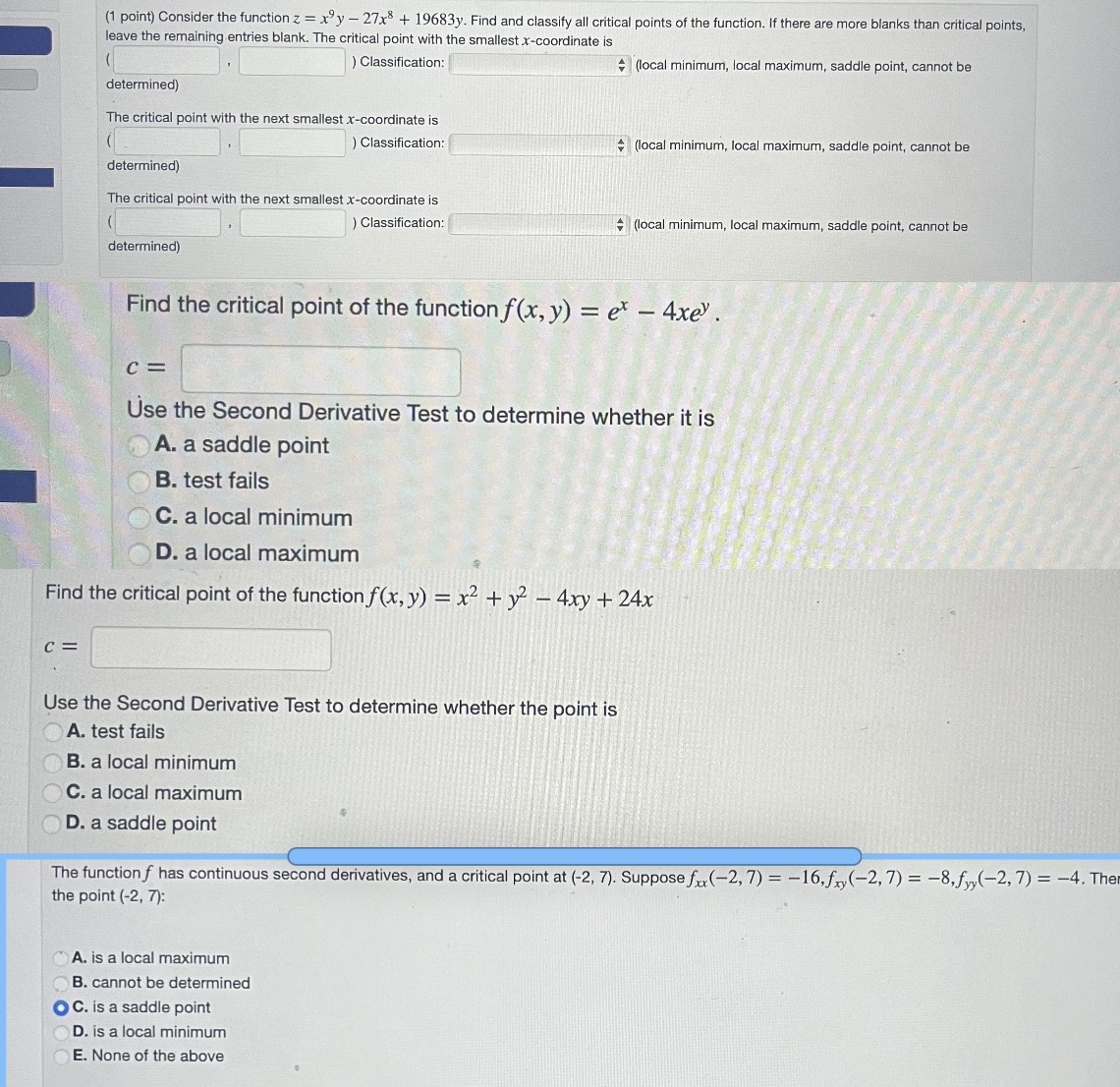
(1 point) Consider the function z = x y - 27x* + 19683y. Find and classify all critical points of the function. If there are more blanks than critical points, leave the remaining entries blank. The critical point with the smallest x-coordinate is ) Classification: * (local minimum, local maximum, saddle point, cannot be determined) The critical point with the next smallest x-coordinate is ) Classification: (local minimum, local maximum, saddle point, cannot be determined) The critical point with the next smallest x-coordinate is ) Classification: (local minimum, local maximum, saddle point, cannot be determined) Find the critical point of the function f(x, y) = ex - 4xey. C= Use the Second Derivative Test to determine whether it is A. a saddle point B. test fails C. a local minimum D. a local maximum Find the critical point of the function f(x, y) = x2 + 32 - 4xy + 24x Use the Second Derivative Test to determine whether the point is A. test fails B. a local minimum C. a local maximum D. a saddle point The function f has continuous second derivatives, and a critical point at (-2, 7). Suppose fax(-2, 7) = -16, fry (-2, 7) = -8, fly(-2, 7) = -4. The the point (-2, 7): A. is a local maximum B. cannot be determined O C. is a saddle point D. is a local minimum E. None of the above