Need help with this differential equation problem

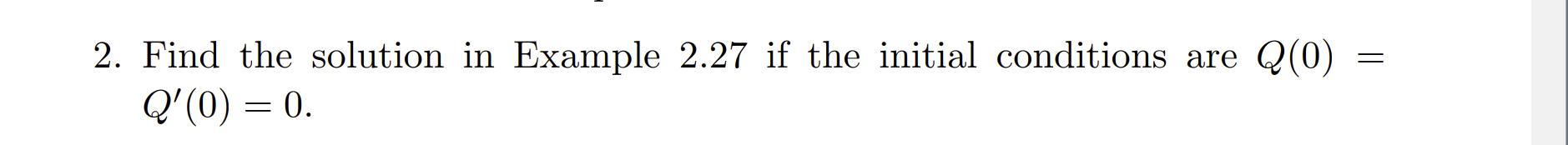
2. Find the solution in Example 2.27 if the initial conditions are 62(0) 2 Q'(0) : 0 Example 2.27 In the previous example, what happens if at = we? Then the general solution in (2.17) is invalid because of division by zero; thus we have to re-solve the problem. The circuit equation is Q" + ng = Sinwgt, (2.19) where the circuit is forced at the same frequency as its natural frequency. The homogeneous solution is the same as before. but the particular solution now has the form Qp(t) = t(A sinwot + 3 cos wet), with a factor of t multiplying the terms. Therefore the general solution of (2.19) has the form (205) = cl cos wot + (:2 sinwgt + t(A sinwot + B cos wot). Without actually determining the constants, we can infer the nature of the response. Because of the t factor in the particular solution, the amplitude of the oscillatory response Q(t) grows in time. This is the phenomenon of pure resonance, or mathematical resonance. It occurs when the frequency of the external force is the same as the natural frequency of the system. The previous example is an ideal case and physically unreasonable. All circuits have resistance, or dissipation, even though it may be small. We ask what happens if we include a small damping term in the circuit and still force it at its natural frequency