Need help with this java Percolation code. I'd appreciate any help, thanks.

TEMPLATE;

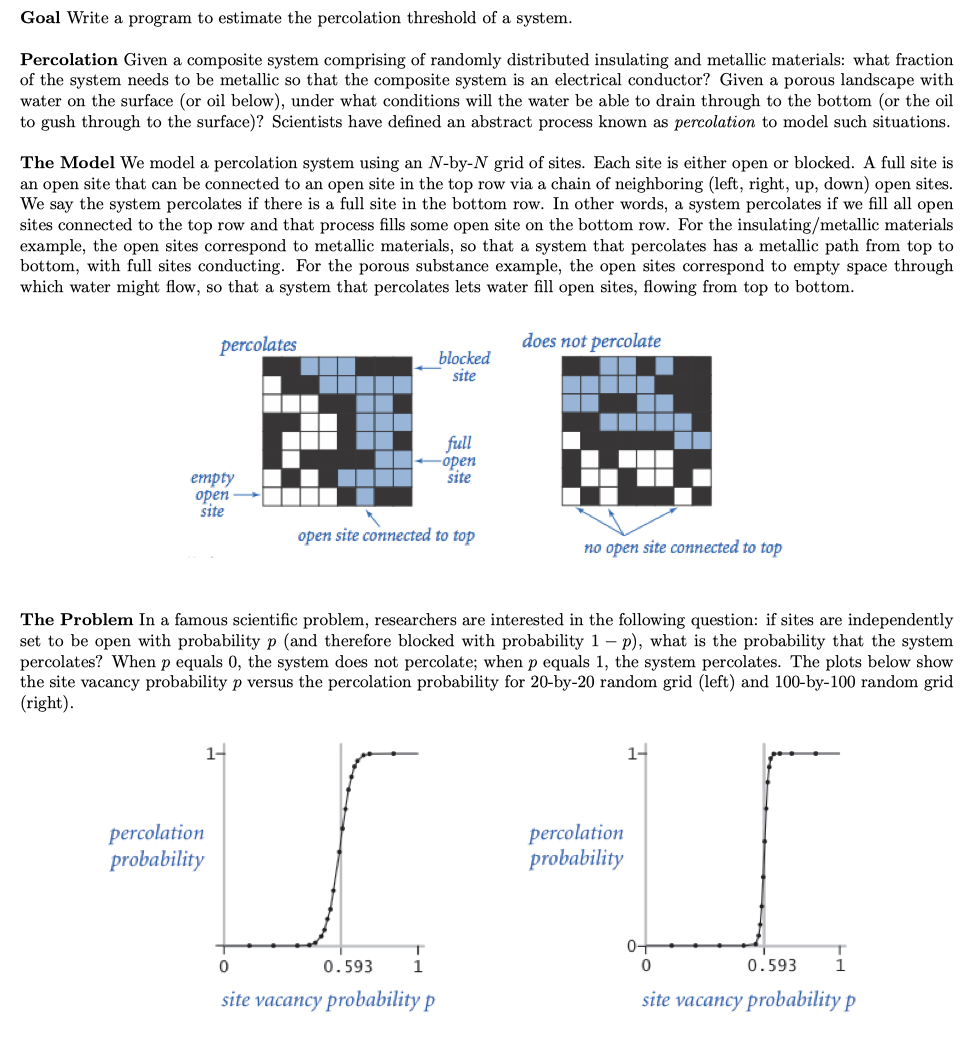
package edu.umb.cs210.p1; import dsa.WeightedQuickUnionUF; import stdlib.In; import stdlib.StdOut; // Models an N-by-N percolation system. public class Percolation { ... // Creates an N-by-N grid, with all sites blocked. public Percolation(int N) { ... } // Opens site (i, j) if it is not open already. public void open(int i, int j) { ... } // Checks if site (i, j) is open. public boolean isOpen(int i, int j) { ... } // Checks if site (i, j) is full. public boolean isFull(int i, int j) { ... } // Returns the number of open sites. public int numberOfOpenSites() { ... } // Checks if the system percolates. public boolean percolates() { ... } // Returns an integer ID (1...N) for site (i, j). protected int encode(int i, int j) { ... } // Test client. [DO NOT EDIT] public static void main(String[] args) { String filename = args[0]; In in = new In(filename); int N = in.readInt(); Percolation perc = new Percolation(N); while (!in.isEmpty()) { int i = in.readInt(); int j = in.readInt(); perc.open(i, j); } StdOut.println(perc.numberOfOpenSites() + " open sites"); if (perc.percolates()) { StdOut.println("percolates"); } else { StdOut.println("does not percolate"); } // Check if site (i, j) optionally specified on the command line // is full. if (args.length == 3) { int i = Integer.parseInt(args[1]); int j = Integer.parseInt(args[2]); StdOut.println(perc.isFull(i, j)); } } } 

Goal Write a program to estimate the percolation threshold of a system. Percolation Given a composite system comprising of randomly distributed insulating and metallic materials: what fraction of the system needs to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations. The Model We model a percolation system using an N-by-N grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom. percolates does not percolate blocked site full open site empty oper site open site connected to top no open site connected to top The Problem in a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1-p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (left) and 100-by-100 random grid (right). percolation probability percolation probability 0.593 0.5931 site vacancy probability p site vacancy probability p When N is sufficiently large, there is a threshold value p* such that when p p*, a random N-by-N grid almost always percolates. No mathematical solution for determining the percolation threshold p* has yet been derived. Your task is to write a computer program to estimate p*. Problem 1. (Model a Percolation System) To model a percolation system, create a data type Percolation in Percolation.java with the following API: Method Description Percolation(int N) creates an N-by-N grid, with all sites blocked void open(int i, int j) opens site (1,1) boolean isOpen (int i, int 1) returns true if site (i, j) is open, and false otherwise boolean isFull(int i, int )) returns true if site ( ii) is full, and false otherwise int numberOfOpenSites() returns the number of open sites boolean percolates() returns true if the system percolates, and false otherwise Corner cases. By convention, the row and column indices i and j are integers between 0 and N -1, where (0,0) is the upper-left site. Throw a java.lang.IndexOutOfBoundsException if any argument to open(), isOpen(), or isFull() is outside its prescribed range. The constructor should throw a java.lang. IllegalArgumentException if N */workspace/projecti $ java edu.umb. cs210. pl. Percolation data/input10.txt 56 open sites percolates $ java edu.umb.cs210.pi. Percolation data/input10-no.txt 55 open sites does not percolate Problem 1. (Model a Percolation System) To model a percolation system, create a data type Percolation with the following API: Method Percolation(int n) void open (int i, int j) boolean isOpen (int i, int j) boolean isFull(int i, int j) Description creates an N-by-N grid, with all sites blocked opens site (i, j) returns true if site (i, j) is open, and false otherwise returns true if site (i, j) is full, and false otherwise returns the number of open sites returns true if the system percolates, and false otherwise int number of OpenSites) boolean percolates () Hints w Model percolation system as an N * N array of booleans (true = open site and false => blocked site) w Can implement the API by scanning the array directly, but that does not meet all the performance requirements; use Union-find (UF) data structure instead my Create an ur object with N2 + 2 sites and use the private encode () method to map sites (0,0), (0, 1), ...,(N 1, N 1) of the array to sites 1, 2, ..., N2 of the ur object; sites 0 (source) and N2 + 1 (sink) are virtual, ie, not part of the percolation system My Instance variables w Percolation system size, int n ws Percolation system, boolean [] [] open my Number of open sites, int openSites my Union-find representation of the percolation system, WeightedQuickUnionUF uf Problems my private int encode(int i, int j) my Return the ur site (1...N) corresponding to the percolation system site (i, j) > public Percolation(int n) my Initialize instance variables my Connect the sites corresponding to first and last rows of the percolation system with the source and sink sites respectively my The 3 x 3 system with its top and bottom row sites connected to the source and sink sites respectively * void open(int i, int j) my Open the site (i, j) if it is not already open my Increment openSites by one my Check if any of the neighbors to the north, east, west, and south of (i, j) is open, and if so, connect the site corresponding to (i, j) with the site corresponding to that neighbor my boolean isOpen(int i, int j) wy Return whether site (i, j) is open or not my boolean isFull(int i, int j) my Return whether site (i, j) is full or not; a site is full if it is open and its corresponding site is connected to the source site + int numberOfOpenSites () my Return the number of open sites my boolean percolates() my Return whether the system percolates or not; the system percolates if the sink site is connected to the source site >- */workspace/project 1 $ java edu.umb.cs210.p1.Percolation data/input10.txt 56 open sites percolates $ java edu.umb. cs210.p1. Percolation data/ input10 - no.txt 55 open sites does not percolate Goal Write a program to estimate the percolation threshold of a system. Percolation Given a composite system comprising of randomly distributed insulating and metallic materials: what fraction of the system needs to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations. The Model We model a percolation system using an N-by-N grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom. percolates does not percolate blocked site full open site empty oper site open site connected to top no open site connected to top The Problem in a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1-p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (left) and 100-by-100 random grid (right). percolation probability percolation probability 0.593 0.5931 site vacancy probability p site vacancy probability p When N is sufficiently large, there is a threshold value p* such that when p p*, a random N-by-N grid almost always percolates. No mathematical solution for determining the percolation threshold p* has yet been derived. Your task is to write a computer program to estimate p*. Problem 1. (Model a Percolation System) To model a percolation system, create a data type Percolation in Percolation.java with the following API: Method Description Percolation(int N) creates an N-by-N grid, with all sites blocked void open(int i, int j) opens site (1,1) boolean isOpen (int i, int 1) returns true if site (i, j) is open, and false otherwise boolean isFull(int i, int )) returns true if site ( ii) is full, and false otherwise int numberOfOpenSites() returns the number of open sites boolean percolates() returns true if the system percolates, and false otherwise Corner cases. By convention, the row and column indices i and j are integers between 0 and N -1, where (0,0) is the upper-left site. Throw a java.lang.IndexOutOfBoundsException if any argument to open(), isOpen(), or isFull() is outside its prescribed range. The constructor should throw a java.lang. IllegalArgumentException if N */workspace/projecti $ java edu.umb. cs210. pl. Percolation data/input10.txt 56 open sites percolates $ java edu.umb.cs210.pi. Percolation data/input10-no.txt 55 open sites does not percolate Problem 1. (Model a Percolation System) To model a percolation system, create a data type Percolation with the following API: Method Percolation(int n) void open (int i, int j) boolean isOpen (int i, int j) boolean isFull(int i, int j) Description creates an N-by-N grid, with all sites blocked opens site (i, j) returns true if site (i, j) is open, and false otherwise returns true if site (i, j) is full, and false otherwise returns the number of open sites returns true if the system percolates, and false otherwise int number of OpenSites) boolean percolates () Hints w Model percolation system as an N * N array of booleans (true = open site and false => blocked site) w Can implement the API by scanning the array directly, but that does not meet all the performance requirements; use Union-find (UF) data structure instead my Create an ur object with N2 + 2 sites and use the private encode () method to map sites (0,0), (0, 1), ...,(N 1, N 1) of the array to sites 1, 2, ..., N2 of the ur object; sites 0 (source) and N2 + 1 (sink) are virtual, ie, not part of the percolation system My Instance variables w Percolation system size, int n ws Percolation system, boolean [] [] open my Number of open sites, int openSites my Union-find representation of the percolation system, WeightedQuickUnionUF uf Problems my private int encode(int i, int j) my Return the ur site (1...N) corresponding to the percolation system site (i, j) > public Percolation(int n) my Initialize instance variables my Connect the sites corresponding to first and last rows of the percolation system with the source and sink sites respectively my The 3 x 3 system with its top and bottom row sites connected to the source and sink sites respectively * void open(int i, int j) my Open the site (i, j) if it is not already open my Increment openSites by one my Check if any of the neighbors to the north, east, west, and south of (i, j) is open, and if so, connect the site corresponding to (i, j) with the site corresponding to that neighbor my boolean isOpen(int i, int j) wy Return whether site (i, j) is open or not my boolean isFull(int i, int j) my Return whether site (i, j) is full or not; a site is full if it is open and its corresponding site is connected to the source site + int numberOfOpenSites () my Return the number of open sites my boolean percolates() my Return whether the system percolates or not; the system percolates if the sink site is connected to the source site >- */workspace/project 1 $ java edu.umb.cs210.p1.Percolation data/input10.txt 56 open sites percolates $ java edu.umb. cs210.p1. Percolation data/ input10 - no.txt 55 open sites does not percolate