NEED HELP WITH THIS MATLAB PROBLEM. I HAVE ATTACHED MY CODE, AND IT GIVES ME ERROR IN ASSESSMENTS. I HAVE TRIED ALL THE CHEGG SOLUTIONS, BUT NONE OF THEM WORKS. DON'T GIVE ME SAME SOLUTION AS ALREADY ON CHEGG. DON'T USE THE FUNCTION THING WHICH IS ALREADY ON CHEGG. NEED A WORKING SOLUTION. WILL UPVOTE IF IT WORKS. THANK YOU

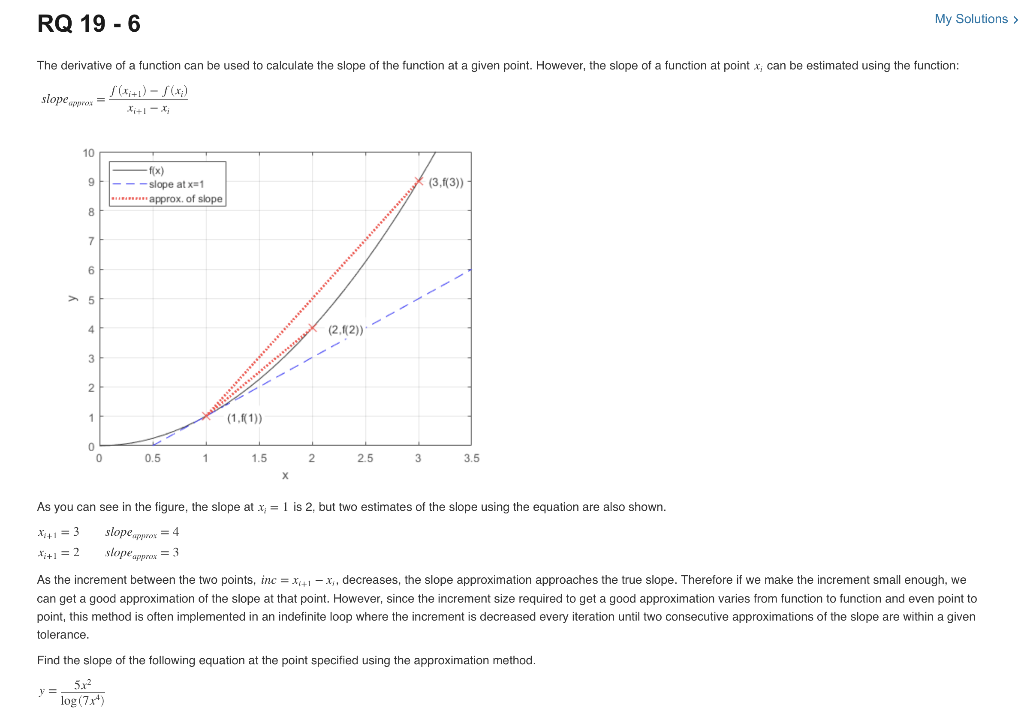
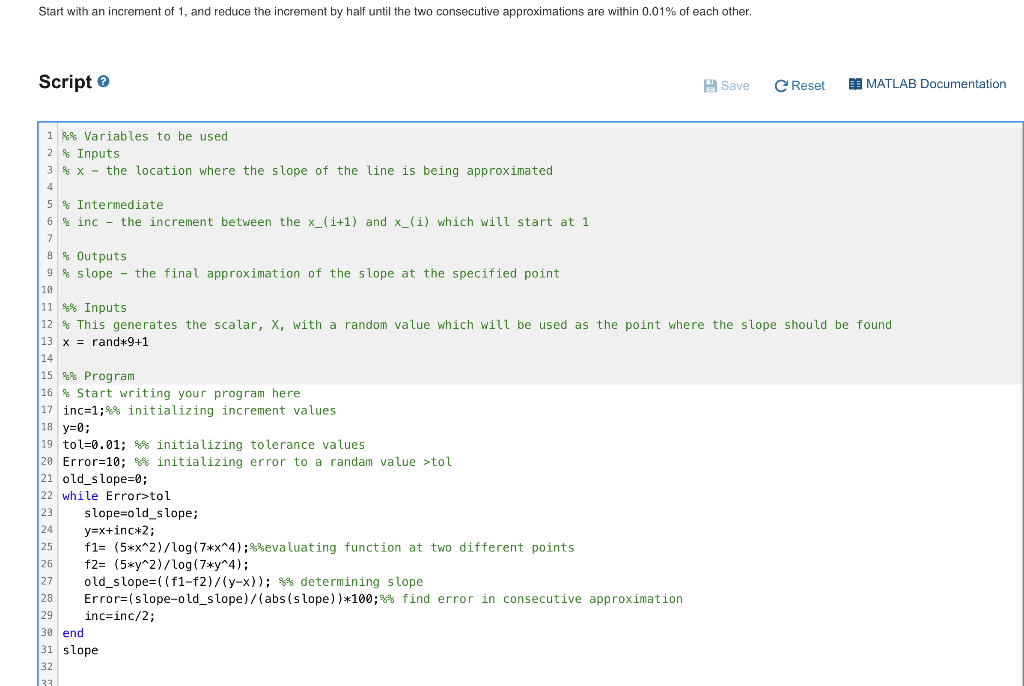
The derivative of a function can be used to calculate the slope of the function at a given point. However, the slope of a function at point xj can be estimated using the function: slopeapprox=xi+1xjf(xi+1)f(xi) As you can see in the figure, the slope at xi=1 is 2 , but two estimates of the slope using the equation are also shown. xi+1=3slopeappyrox=4xi+1=2slopeapprex=3 As the increment between the two points, inc =xi+1xj, decreases, the slope approximation approaches the true slope. Therefore if we make the increment small enough, we can get a good approximation of the slope at that point. However, since the increment size required to get a good approximation varies from function to function and even point to point, this method is often implemented in an indefinite loop where the increment is decreased every iteration until two consecutive approximations of the slope are within a given tolerance. Find the slope of the following equation at the point specified using the approximation method. y=log(7x4)5x2 Start with an increment of 1 , and reduce the increment by half until the two consecutive approximations are within 0.01% of each other. Script 0 Previous Assessment: 1 of 2 Tests Passed (33\%) While Loop Check 33%(33%) Slope 0%(67%) Variable slope has an incorrect value. Your final value of slope is incorrect. Make sure: - The equations for the function and estimation are typed correctly. - The increment started at 1 and was decreased by half each time. - The tolerance was set correctly. Remember that the tolerance was a percent difference rather than an absolute difference