Need the code for the function (ie where it says, "YOUR CODE HERE"). Must run smoothly according to tests. No additional code needed (ie besides the code after "YOUR CODE HERE").

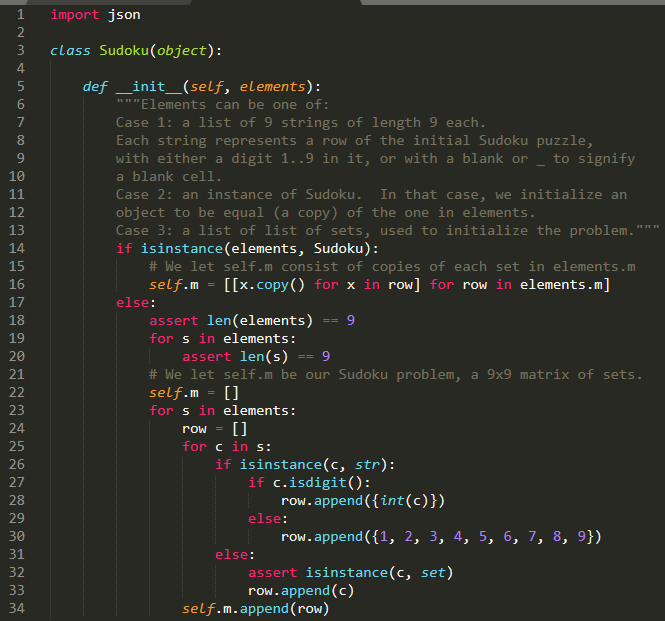
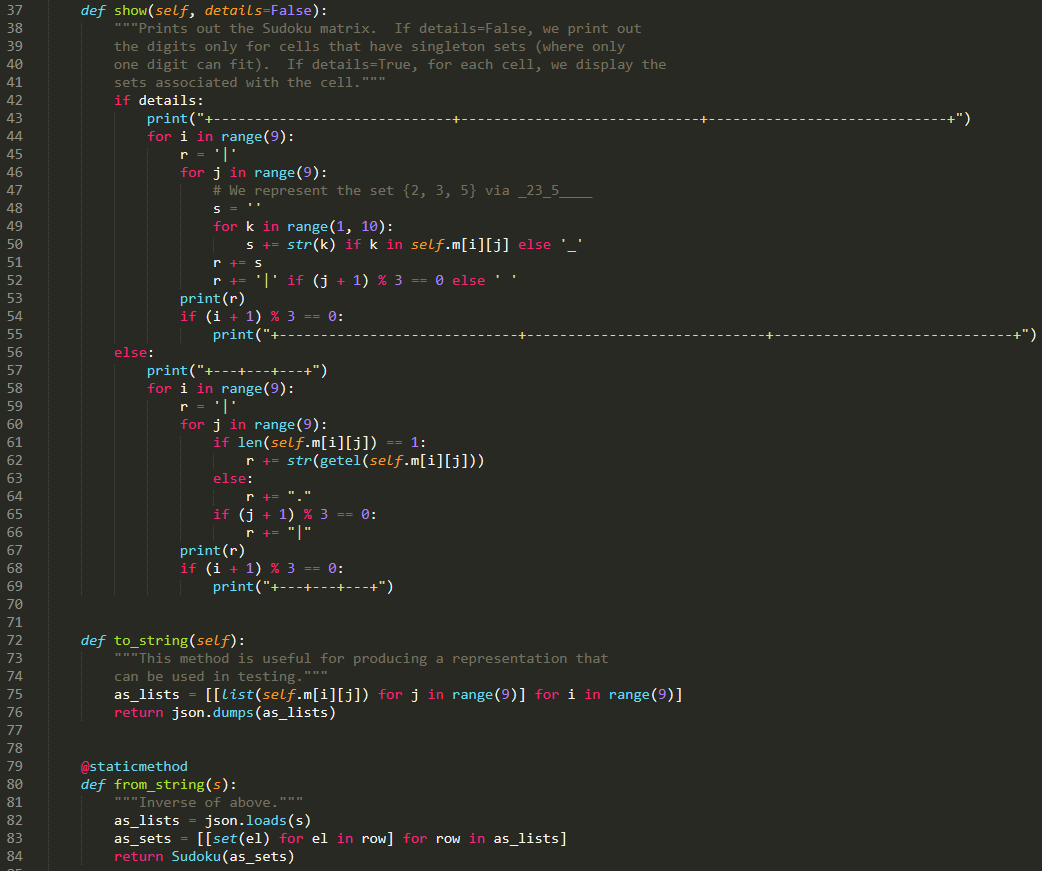
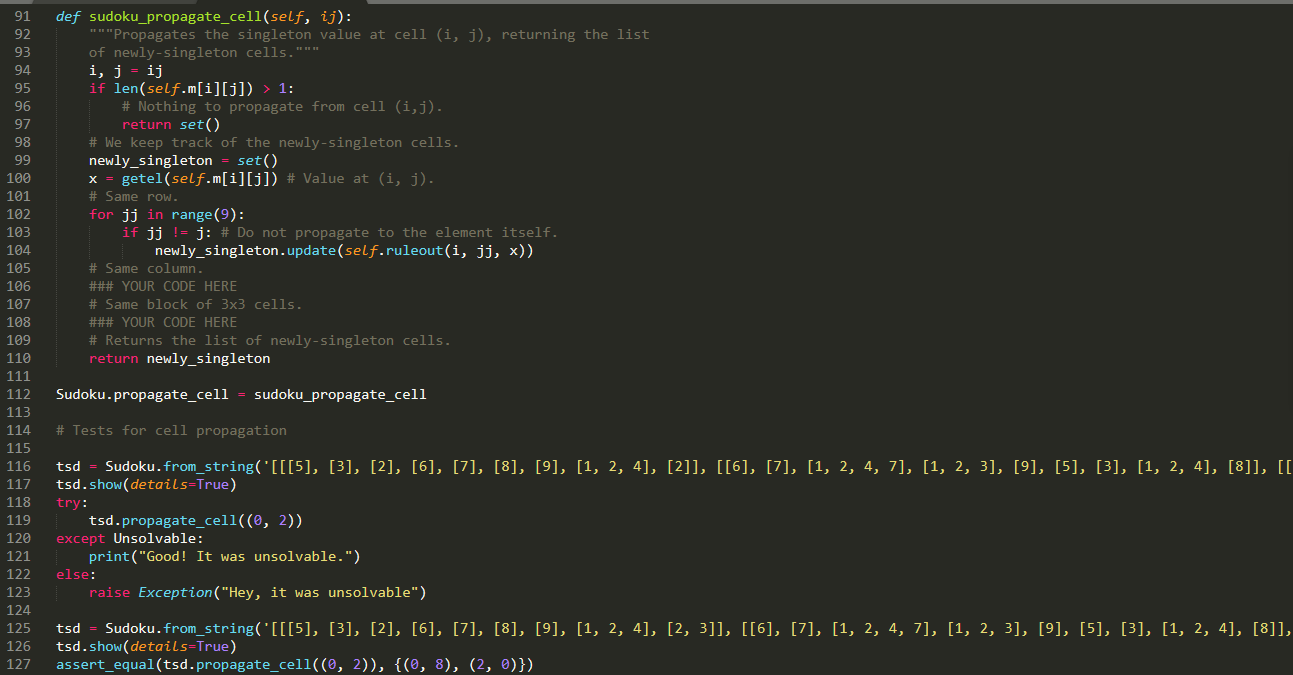
def sudoku_propagate_cell(self, ij):

"""Propagates the singleton value at cell (i, j), returning the list

of newly-singleton cells."""

i, j = ij

if len(self.m[i][j]) > 1:

# Nothing to propagate from cell (i,j).

return set()

# We keep track of the newly-singleton cells.

newly_singleton = set()

x = getel(self.m[i][j]) # Value at (i, j).

# Same row.

for jj in range(9):

if jj != j: # Do not propagate to the element itself.

newly_singleton.update(self.ruleout(i, jj, x))

# Same column.

### YOUR CODE HERE

# Same block of 3x3 cells.

### YOUR CODE HERE

# Returns the list of newly-singleton cells.

return newly_singleton

Sudoku.propagate_cell = sudoku_propagate_cell

import json 1 2 3 4 5 class Sudoku(object): 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 def __init_(self, elements): "Elements can be one of: Case 1: a list of 9 strings of length 9 each. Each string represents a row of the initial Sudoku puzzle, with either a digit 1..9 in it, or with a blank or _ to signify a blank cell. Case 2: an instance of Sudoku. In that case, we initialize an object to be equal (a copy) of the one in elements. Case 3: list of list of sets, used to initialize the problem.' if isinstance(elements, Sudoku): # We let self.m consist of copies of each set in elements.m self.m [[x.copy() for x in row] for row in elements.m] else: assert len(elements) 9 for s in elements: assert len(s) 9 # We let self.m be our Sudoku problem, a 9x9 matrix of sets. self.m = [] for s in elements: row = [] for c in s: if isinstance(c, str): if c.isdigit(): row.append({int(c)}) else: row.append({1, 2, 3, 4, 5, 6, 7, 8, 9}) else: assert isinstance(c, set) row.append(c) self.m.append(row) +") r += S 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 def show(self, details=False): *** Prints out the Sudoku matrix. If details=False, we print out the digits only for cells that have singleton sets (where only one digit can fit). If details=True, for each cell, we display the sets associated with the cell." if details: print("+ for i in range(9): r = 'T for j in range(9): # We represent the set {2, 3, 5} via _23_5_ s=" for k in range(1, 10): s += str(k) if k in self.m[i][j] else '_' r += '1' if (j + 1) % 3 == o else print(r) if (i + 1) % 3 == 0: print("+ else: print("+---+---+---+") for i in range(9): r = 1 for j in range(9): if len(self.m[i][j]) == 1: r += str(getel(self.m[i][j])) else: r += "." if ( + 1) % 3 == 0: r += "" print(r) if (i + 1) % 3 == 0: print("+---+---+---+") +") def to_string(self): **"This method is useful for producing a representation that can be used in testing. "**** as_lists [[list (self.m[i][j]) for j in range(9)] for i in range (9)] return json.dumps (as_lists) 78 79 80 81 82 83 84 @staticmethod def from_string(s): ***"Inverse of above. "**** as_lists json.loads(s) as_sets [[set(el) for el in row] for row in as_lists] return Sudoku(as_sets) 87 88 89 def eq_(self, other): *** "Useful for testing. return self.m other.m 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 def sudoku_propagate_cell(self, ij): ****Propagates the singleton value at cell (i, j), returning the list of newly-singleton cells. """ i, j = ij if len(self.m[i][j]) > 1: # Nothing to propagate from cell (i,j). return set() # We keep track of the newly-singleton cells. newly_singleton set() getel(self.m[i][j]) # Value at (i, j). # Same row. for jj in range(9): if jj != j: # Do not propagate to the element itself. newly_singleton.update(self.ruleout(i, jj, x)) # Same column. ### YOUR CODE HERE # Same block of 3x3 cells. ### YOUR CODE HERE # Returns the list of newly-singleton cells. return newly_singleton Sudoku.propagate_cell sudoku_propagate_cell # Tests for cell propagation tsd Sudoku.from_string('[[[5], [3], [2], [6], [7], [8], [9], [1, 2, 4], [2]], [[6], [7], [1, 2, 4, 7], [1, 2, 3], [9], [5], [3], [1, 2, 4], [8]], [[ tsd.show(details=True) try: tsd.propagate_cell((2, 2)) except Unsolvable: print("Good! It was unsolvable.") else: raise Exception("Hey, it was unsolvable") tsd Sudoku.from_string('[[[5], [3], [2], [6], [7], [8], [9], [1, 2, 4], [2, 3]], [[6], [7], [1, 2, 4, 7], [1, 2, 3], [9], [5], [3], [1, 2, 4], [8]], tsd.show(details=True) assert_equal(tsd.propagate_cell((0, 2)), {(0, 8), (2, 0)}) import json 1 2 3 4 5 class Sudoku(object): 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 def __init_(self, elements): "Elements can be one of: Case 1: a list of 9 strings of length 9 each. Each string represents a row of the initial Sudoku puzzle, with either a digit 1..9 in it, or with a blank or _ to signify a blank cell. Case 2: an instance of Sudoku. In that case, we initialize an object to be equal (a copy) of the one in elements. Case 3: list of list of sets, used to initialize the problem.' if isinstance(elements, Sudoku): # We let self.m consist of copies of each set in elements.m self.m [[x.copy() for x in row] for row in elements.m] else: assert len(elements) 9 for s in elements: assert len(s) 9 # We let self.m be our Sudoku problem, a 9x9 matrix of sets. self.m = [] for s in elements: row = [] for c in s: if isinstance(c, str): if c.isdigit(): row.append({int(c)}) else: row.append({1, 2, 3, 4, 5, 6, 7, 8, 9}) else: assert isinstance(c, set) row.append(c) self.m.append(row) +") r += S 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 def show(self, details=False): *** Prints out the Sudoku matrix. If details=False, we print out the digits only for cells that have singleton sets (where only one digit can fit). If details=True, for each cell, we display the sets associated with the cell." if details: print("+ for i in range(9): r = 'T for j in range(9): # We represent the set {2, 3, 5} via _23_5_ s=" for k in range(1, 10): s += str(k) if k in self.m[i][j] else '_' r += '1' if (j + 1) % 3 == o else print(r) if (i + 1) % 3 == 0: print("+ else: print("+---+---+---+") for i in range(9): r = 1 for j in range(9): if len(self.m[i][j]) == 1: r += str(getel(self.m[i][j])) else: r += "." if ( + 1) % 3 == 0: r += "" print(r) if (i + 1) % 3 == 0: print("+---+---+---+") +") def to_string(self): **"This method is useful for producing a representation that can be used in testing. "**** as_lists [[list (self.m[i][j]) for j in range(9)] for i in range (9)] return json.dumps (as_lists) 78 79 80 81 82 83 84 @staticmethod def from_string(s): ***"Inverse of above. "**** as_lists json.loads(s) as_sets [[set(el) for el in row] for row in as_lists] return Sudoku(as_sets) 87 88 89 def eq_(self, other): *** "Useful for testing. return self.m other.m 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 def sudoku_propagate_cell(self, ij): ****Propagates the singleton value at cell (i, j), returning the list of newly-singleton cells. """ i, j = ij if len(self.m[i][j]) > 1: # Nothing to propagate from cell (i,j). return set() # We keep track of the newly-singleton cells. newly_singleton set() getel(self.m[i][j]) # Value at (i, j). # Same row. for jj in range(9): if jj != j: # Do not propagate to the element itself. newly_singleton.update(self.ruleout(i, jj, x)) # Same column. ### YOUR CODE HERE # Same block of 3x3 cells. ### YOUR CODE HERE # Returns the list of newly-singleton cells. return newly_singleton Sudoku.propagate_cell sudoku_propagate_cell # Tests for cell propagation tsd Sudoku.from_string('[[[5], [3], [2], [6], [7], [8], [9], [1, 2, 4], [2]], [[6], [7], [1, 2, 4, 7], [1, 2, 3], [9], [5], [3], [1, 2, 4], [8]], [[ tsd.show(details=True) try: tsd.propagate_cell((2, 2)) except Unsolvable: print("Good! It was unsolvable.") else: raise Exception("Hey, it was unsolvable") tsd Sudoku.from_string('[[[5], [3], [2], [6], [7], [8], [9], [1, 2, 4], [2, 3]], [[6], [7], [1, 2, 4, 7], [1, 2, 3], [9], [5], [3], [1, 2, 4], [8]], tsd.show(details=True) assert_equal(tsd.propagate_cell((0, 2)), {(0, 8), (2, 0)})