need this program to be written in C

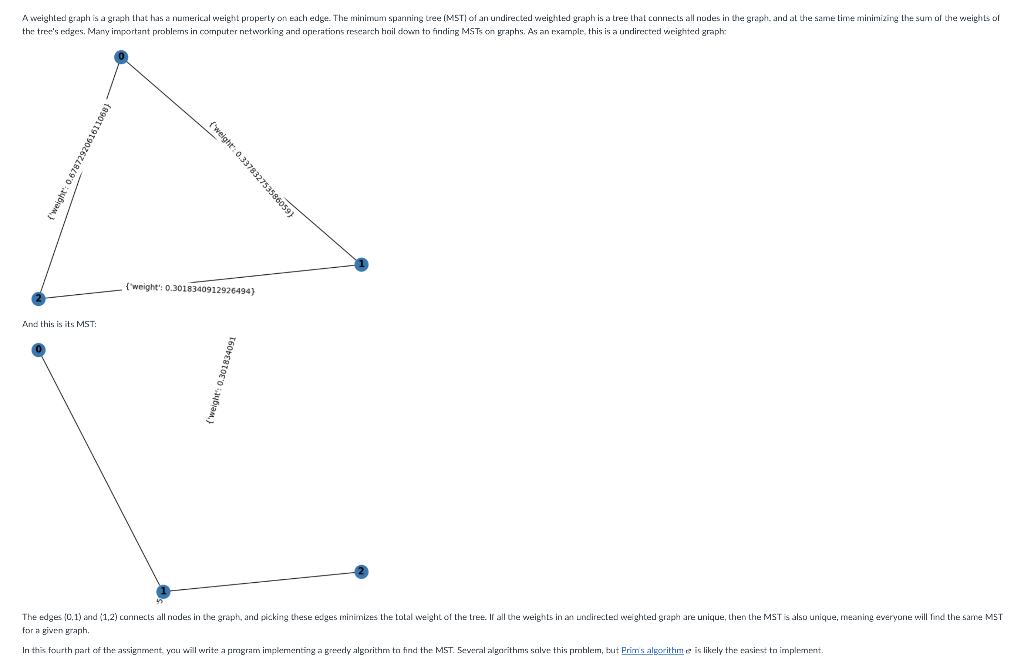
A weighted graph is a graph that has a numerical weight properly on each edge. The minimum spanning tree (MST) of an undirected weighted graph is a tree that connects all nodes in the graph, and at the same time minimizing the sum of the weights of the tree's edges. Many important problems in computer networking and operations research hoil down to inding MSTs on graphs. As an example, this is a undirected weighted graph: {" weight (65098SESLZEBLEED {"weight": 0.3018340912926494) And this is its MST: weight: 0.301834091 The edges (0,1) and (1,2) connects all nodes in the graph, and picking these edges minimizes the total weight of the tree. If all the weights in an undirected weighted graph are unique, then the MST is also unique, meaning everyone will find the same MST for a given graph. In this fourth part of the assignment, you will write a program implementing a greedy algorithm to find the MST. Several algorithms salve this problem, but Prims algorithme is likely the easiest to implement Input format Your program should take a single command line argument specifying the path to an input file. Test cases for your program are in the tests/ directory. In each test case, the first line records the number of nodes N in the graph. Then, the adjacency matrix is recorded in the subsequent N rows of the file. This time, the adjacency matrix contains floating point numbers. 0.0 indicates no edge between two nodes. Any other value indicates an edge with the given value as the edge weight. Output format Expected outputs from your program for each test case are in the answers/ directory. You should print a list of edges that, taken together, form the MST of the input graph. Again, the ordering of the nodes in each edge does not matter. The ordering of the edges does not matter