Need to fix the python codes: (Change my codes using generator and yield method)

Given Codes:

Problem and my codes:

Text:

class CountingQueue(object):

def __init__(self):

self.queue = []

def __repr__(self):

return repr(self.queue)

def add(self, x, count=1):

# If the element is the same as the last element, we simply

# increment the count. This assumes we can test equality of

# elements.

if len(self.queue) > 0:

xx, cc = self.queue[-1]

if xx == x:

self.queue[-1] = (xx, cc + count)

else:

self.queue.append((x, count))

else:

self.queue = [(x, count)]

def get(self):

if len(self.queue) == 0:

return None

x, c = self.queue[0]

if c == 1:

self.queue.pop(0)

return x

else:

self.queue[0] = (x, c - 1)

return x

def isempty(self):

# Since the count of an element is never 0, we can just check

# whether the queue is empty.

return len(self.queue) == 0

My codes(Change this to generator and use yield method):

def countingqueue_len(self):

a=0

for i in self.queue:

a+=i[1]

return a

# This is a way to add a method to a class once the class

# has already been defined.

CountingQueue.__len__ = countingqueue_len

### Tests for `__len__`

from nose.tools import assert_equal

q = CountingQueue()

for i in range(10):

q.add('a')

q.add('b')

for i in range(3):

q.add('c', count=2)

assert_equal(len(q), 17)

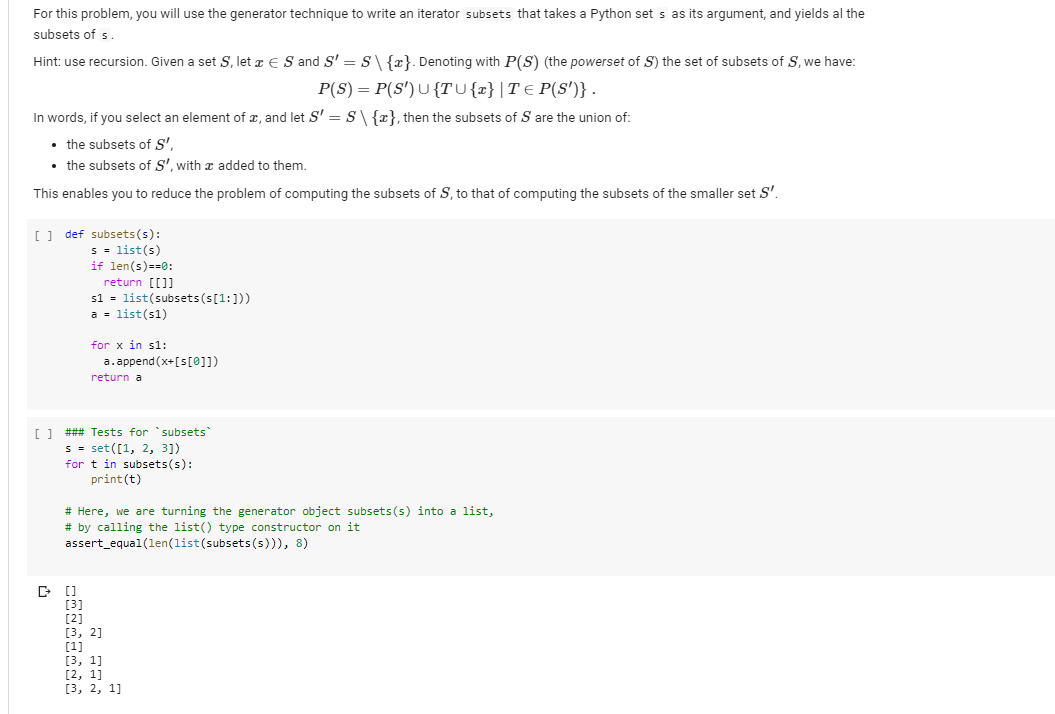
[ ] class CountingQueue(object): def __init__(self): self.queue = [] def _repr_(self): return repr(self.queue) def add(self, x, count=1): # If the element is the same as the last element, we simply # increment the count. This assumes we can test equality of # elements. if len(self.queue) > 0: XX, CC = self.queue[-1] if xx == X: self.queue[-1] = (xx, CC + count) else: self.queue.append((x, count)) else: self.queue = [(x, count)] def get(self): if len(self.queue) == 0: return None X, C = self.queue[@] if c == 1: self.queue.pop() return x else: self.queue[@] = (x, C-1) return x def isempty(self): # Since the count of an element is never e, we can just check # whether the queue is empty. return len(self.queue) == 0 For this problem, you will use the generator technique to write an iterator subsets that takes a Python set s as its argument, and yields al the subsets of s. Hint: use recursion. Given a set S, let ze S and S' =S {c}. Denoting with P(S) (the powerset of S) the set of subsets of S, we have: P(S) = P(S') {TU{2}|TE P(S')} . In words, if you select an element of c, and let S' =S {2}, then the subsets of S are the union of: the subsets of S'. the subsets of S', with x added to them. This enables you to reduce the problem of computing the subsets of S, to that of computing the subsets of the smaller set S'. [ ] def subsets(s): s = list(s) if len(s) ==0: return [[]] sl = list (subsets(S(1:])) a = list (51) for x in s1: a.append(x+[S[@]]) return a [] ### Tests for "subsets S = set([1, 2, 3]) for t in subsets(s): print(t) # Here, we are turning the generator object subsets(s) into a list, # by calling the list type constructor on it assert_equal(len(list (subsets(s))), 8) [3, 2] [3, 1] [2, 1] (3, 2, 1] [ ] class CountingQueue(object): def __init__(self): self.queue = [] def _repr_(self): return repr(self.queue) def add(self, x, count=1): # If the element is the same as the last element, we simply # increment the count. This assumes we can test equality of # elements. if len(self.queue) > 0: XX, CC = self.queue[-1] if xx == X: self.queue[-1] = (xx, CC + count) else: self.queue.append((x, count)) else: self.queue = [(x, count)] def get(self): if len(self.queue) == 0: return None X, C = self.queue[@] if c == 1: self.queue.pop() return x else: self.queue[@] = (x, C-1) return x def isempty(self): # Since the count of an element is never e, we can just check # whether the queue is empty. return len(self.queue) == 0 For this problem, you will use the generator technique to write an iterator subsets that takes a Python set s as its argument, and yields al the subsets of s. Hint: use recursion. Given a set S, let ze S and S' =S {c}. Denoting with P(S) (the powerset of S) the set of subsets of S, we have: P(S) = P(S') {TU{2}|TE P(S')} . In words, if you select an element of c, and let S' =S {2}, then the subsets of S are the union of: the subsets of S'. the subsets of S', with x added to them. This enables you to reduce the problem of computing the subsets of S, to that of computing the subsets of the smaller set S'. [ ] def subsets(s): s = list(s) if len(s) ==0: return [[]] sl = list (subsets(S(1:])) a = list (51) for x in s1: a.append(x+[S[@]]) return a [] ### Tests for "subsets S = set([1, 2, 3]) for t in subsets(s): print(t) # Here, we are turning the generator object subsets(s) into a list, # by calling the list type constructor on it assert_equal(len(list (subsets(s))), 8) [3, 2] [3, 1] [2, 1] (3, 2, 1]