Needing help correct this practice question.

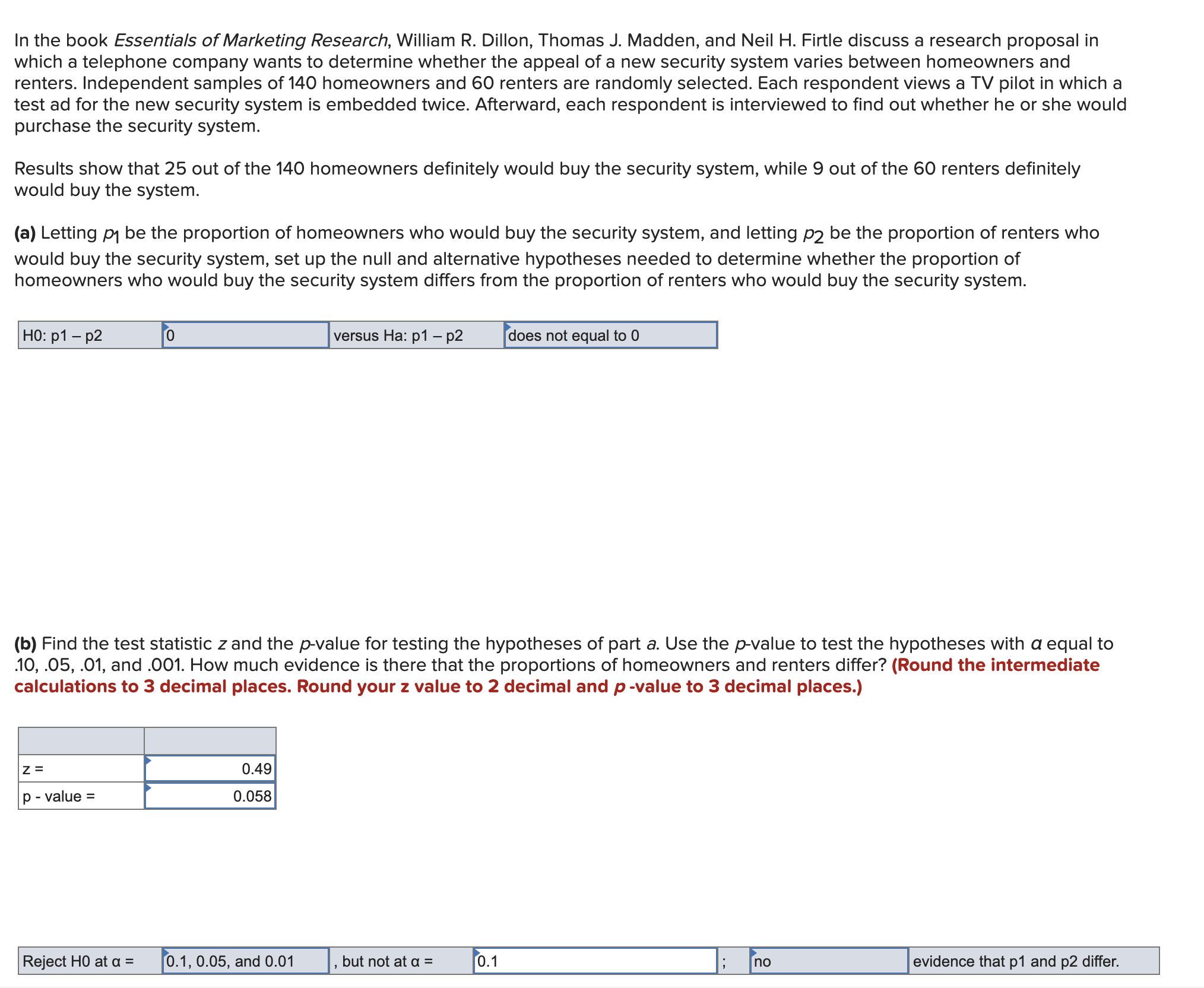
In the book Essentials ofMarketing Research, William R. Dillon, Thomas J. Madden, and Neil H. Firtle discuss a research proposal in which a telephone company wants to determine whether the appeal of a new security system varies between homeowners and renters. Independent samples of 140 homeowners and 60 renters are randomly selected. Each respondent views a TV pilot in which a test ad for the new security system is embedded twice. Afterward, each respondent is interviewed to nd out whether he or she would purchase the security system. Results show that 25 out ofthe 140 homeowners definitely would buy the security system, while 9 out ofthe 60 renters denitely would buy the system. (a) Letting p1 be the proportion of homeowners who would buy the security system, and letting p2 be the proportion of renters who would buy the security system, set up the null and alternative hypotheses needed to determine whether the proportion of homeowners who would buy the security system differs from the proportion of renters who would buy the security system. H0: p1 p2 _ versus Ha: p1 p2 does not equal to 0 (b) Find the test statistic z and the p-value for testing the hypotheses of part a. Use the p-value to test the hypotheses with 0 equal to .10, .05, .01, and .001. How much evidence is there that the proportions of homeowners and renters differ? (Round the intermediate calculations to 3 decimal places. Round your 2 value to 2 decimal and p -value to 3 decimal places.) 2: p - value = Reject H0 at a = 0.1, 0.05, and 0.01 , but not at a = _-_ evidence that p1 and p2 differ. (c) Calculate a 95 percent confidence interval for the difference between the proportions of homeowners and renters who would buy the security system. On the basis of this interval, can we be 95 percent confident that these proportions differ? (Round your answers to confidence interval to 4 decimal places. Negative amounts should be indicated by a minus sign. ) Condence interval = [ (0.0818). 0.1390 1