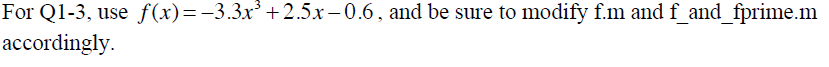
Newton.m

function newton(f,df,x0,tol,n)

% Newton's method for solving the nonlinear

% equation f(x)=0.

iter=0;

u=feval(f,x0);

v=feval(df,x0);

err=abs(u/v);

disp('___________________________________________________')

disp(' iter x f(x) df(x) |xn+1-xn|')

disp('___________________________________________________')

fprintf('%2.0f %12.6f %12.6f %12.6f ',iter,x0,u,v)

while (err>tol)&(iter

x1=x0-u/v;

err=abs(x1-x0);

x0=x1;

u=feval(f,x0);

v=feval(df,x0);

iter=iter+1;

fprintf('%2.0f %12.6f %12.6f %12.6f %12.6f ',iter,x0,u,v,err)

end

if (v==0)

disp(' division by zero')

end

if (iter>n)

disp(' Method failed to converge')

end

.............................................................................................................................

Secant.m

function secant(f,x0,x1,tol,n)

% The secant method for solving the nonlinear

% equation f(x)=0.

iter=0;

u=feval(f,x0);

v=feval(f,x1);

err=abs(x1-x0);

disp('______________________________________________________________')

disp('iter xn f(xn) f(xn+1)-f(xn) |xn+1-xn|')

disp('______________________________________________________________')

fprintf('%2.0f %12.6f %12.6f ',iter,x0,u)

fprintf('%2.0f %12.6f %12.6f %12.6f %12.6f ',iter,x1,v,v-u,err)

while (err>tol)&(iter

x=x1-v*(x1-x0)/(v-u);

x0=x1;

u=v;

x1=x;

v=feval(f,x1);

err=abs(x1-x0);

iter=iter+1;

fprintf('%2.0f %12.6f %12.6f %12.6f %12.6f ',iter,x1,v,v-u,err)

end

if ((v-u)==0)

disp(' Division by zero')

end

if (iter>n)

disp(' Method failed to converge')

end

For 01-3, use f (x)E-3.3x3 +2.5x -0.6, and be sure to modify f m and f and fprime.m accordingly