Neyman - Pearson Lemma (Theorem).

Here is a proof for a case of continous variables. Below the photos are showing proof for continous random variables.Question: Please give a proof for DISCRETE variables which can be achieved by replacing integrals with sums.

?

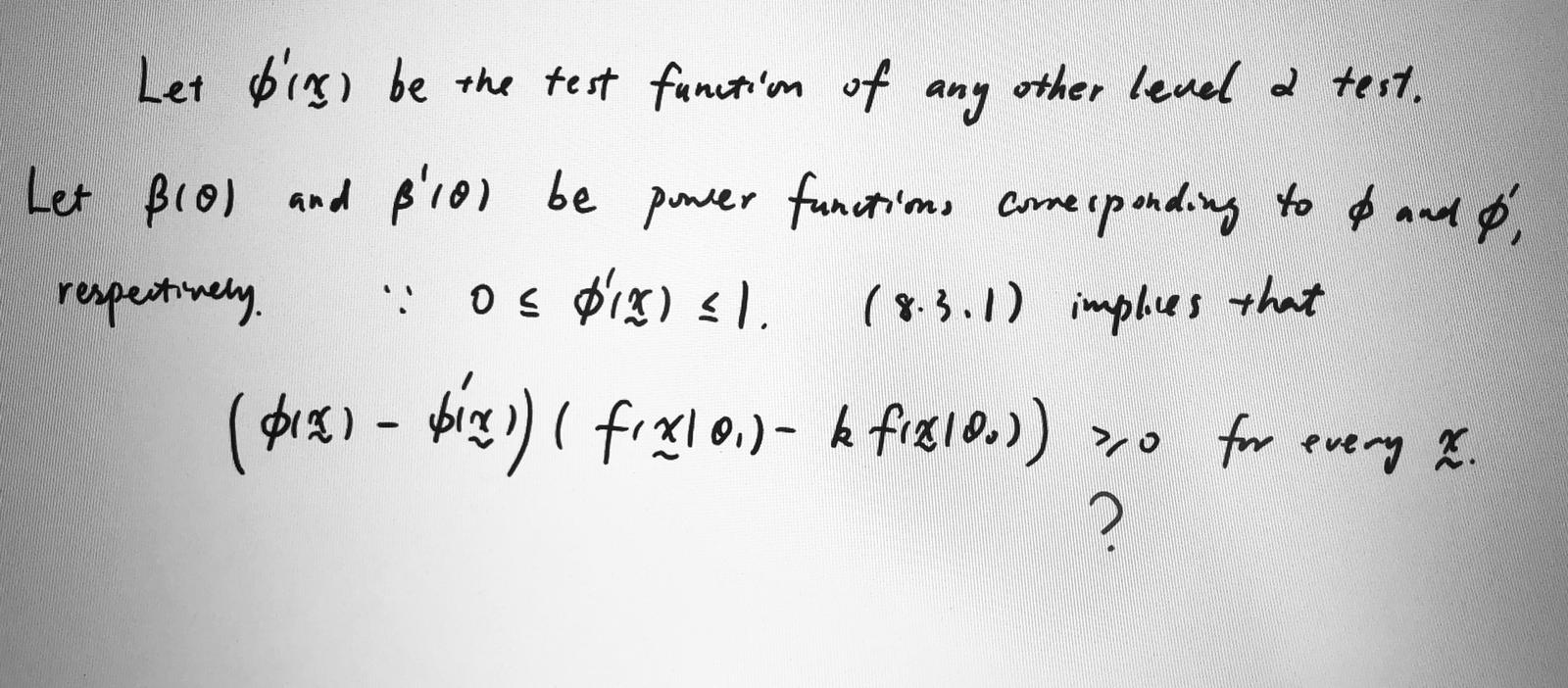
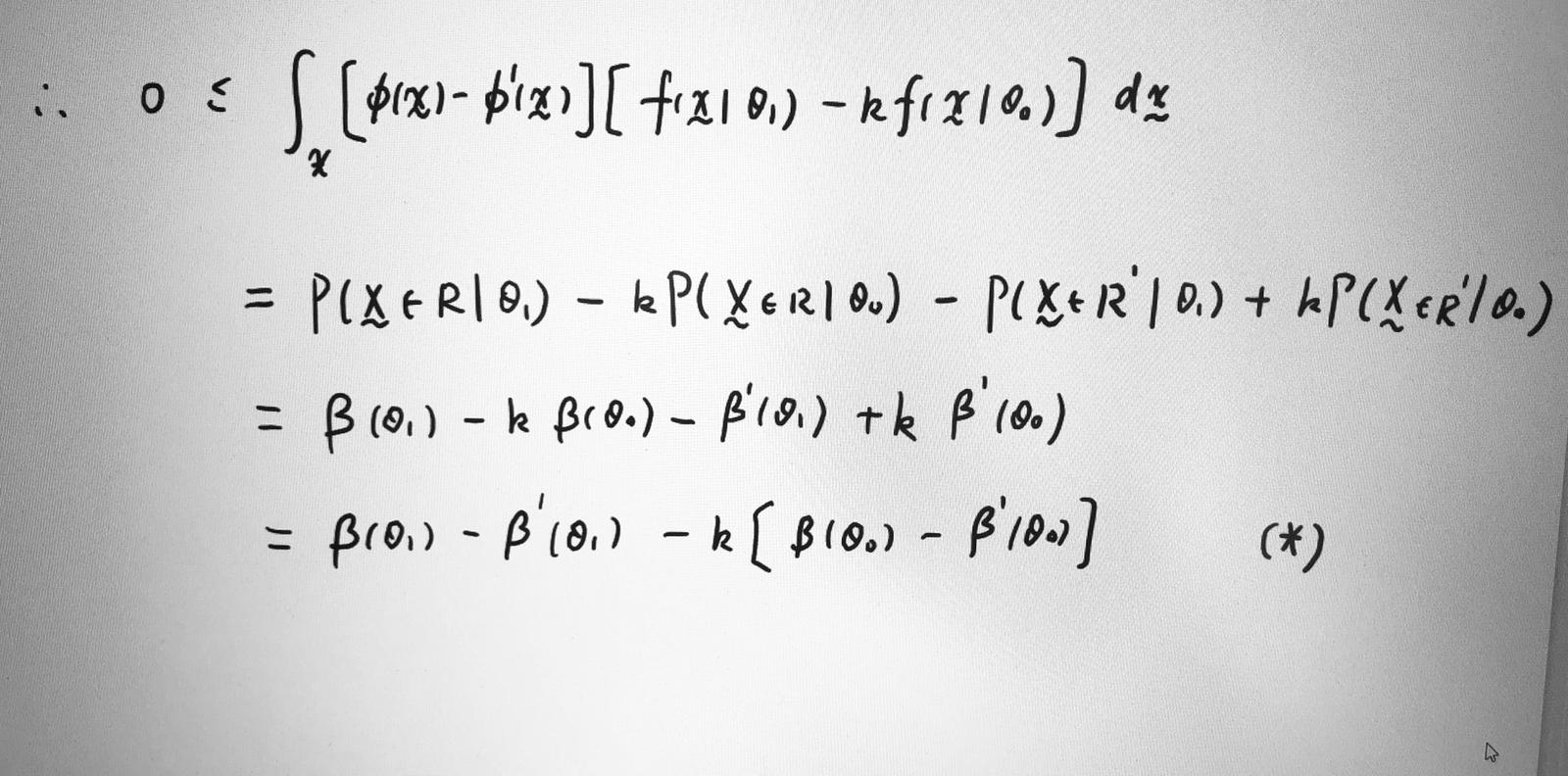
Let big) be the test function of any other level a test. Let BIO) and Blo) be power functions corresponding to go and of respectively . .: 0 5 0 12) =1. ( 8 . 3 . 1) implies that ($1=) - bix) ) ( fixlo,) - 62fixlo.) ) so for every 2.Proof Continuous X ( discrete ? ) ( a ) . Define a test function $ (x ) = s 1, X ER . , Z ER where R satisfies 18.3. 1) & 18. 3. 2 ) Note any test satisfying (8. 3. 2 ) is a size a test, hence, a level of test.\f