NO NEED FOR A EXPLANATION, JUST ANSWER ONLY.

Q1.

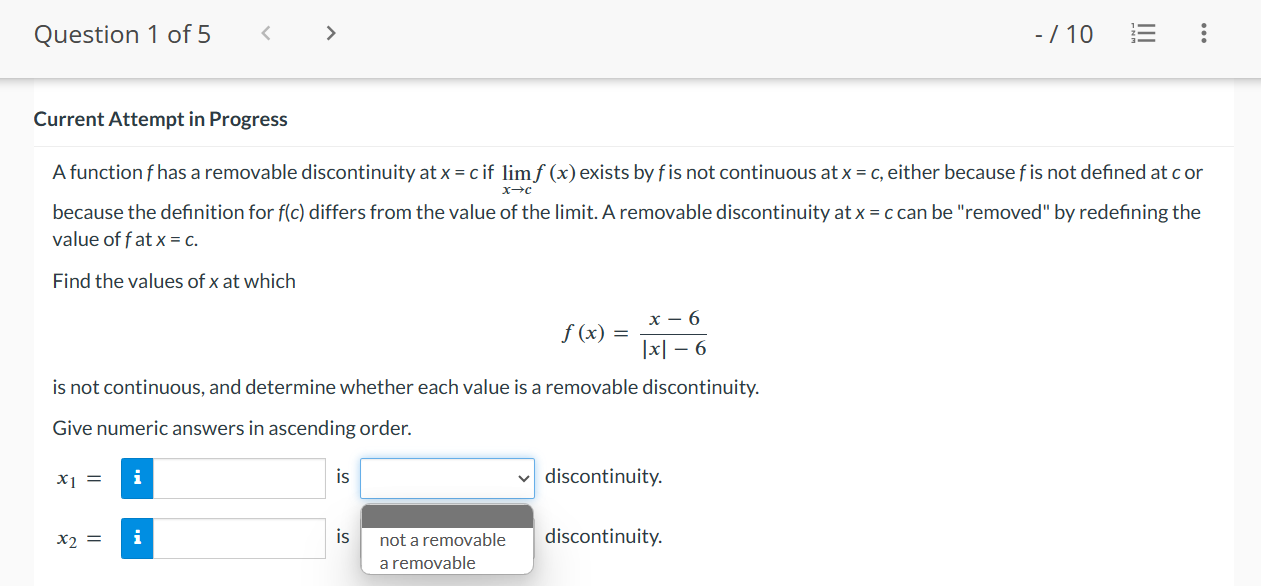
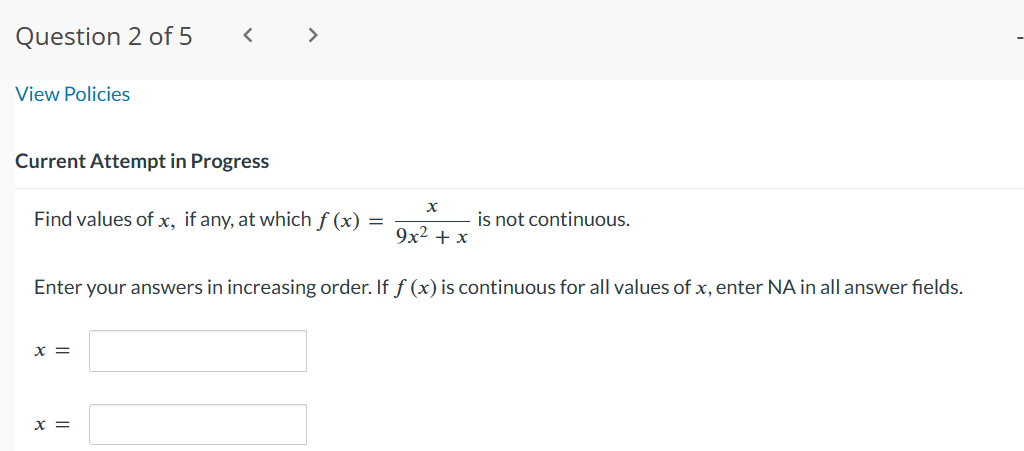
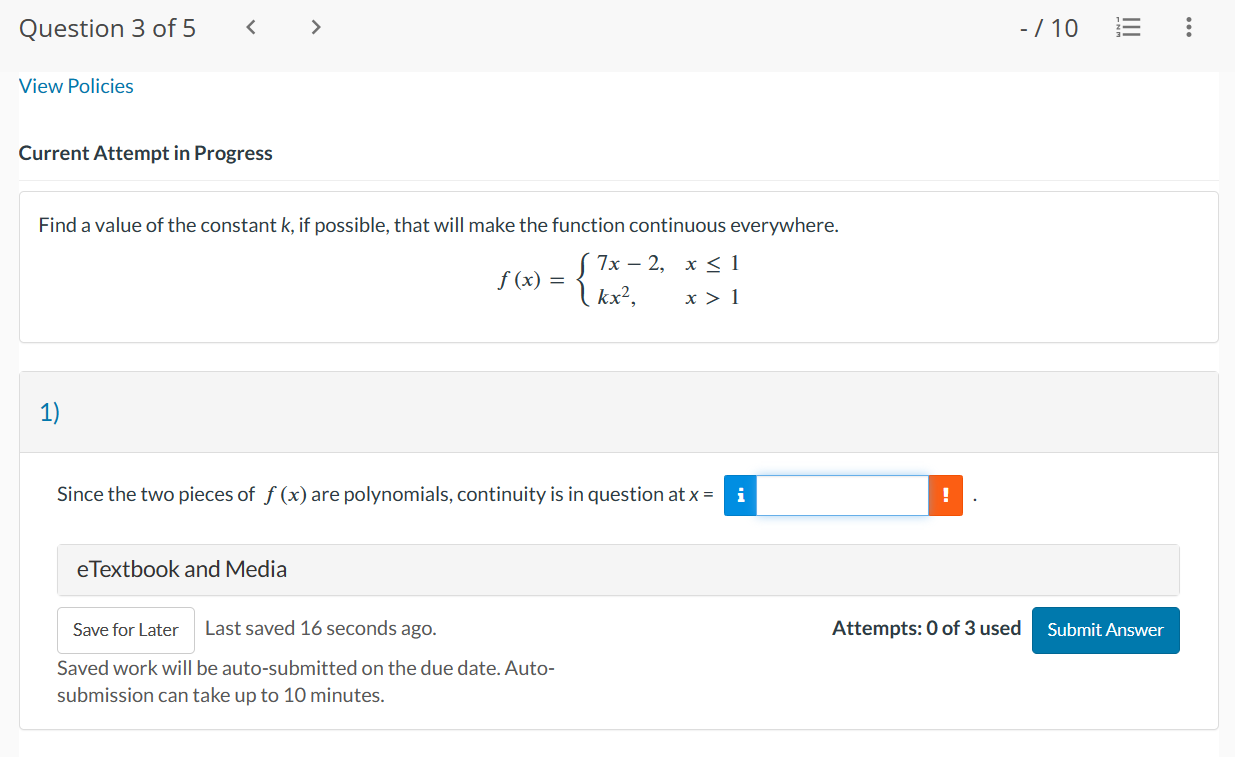
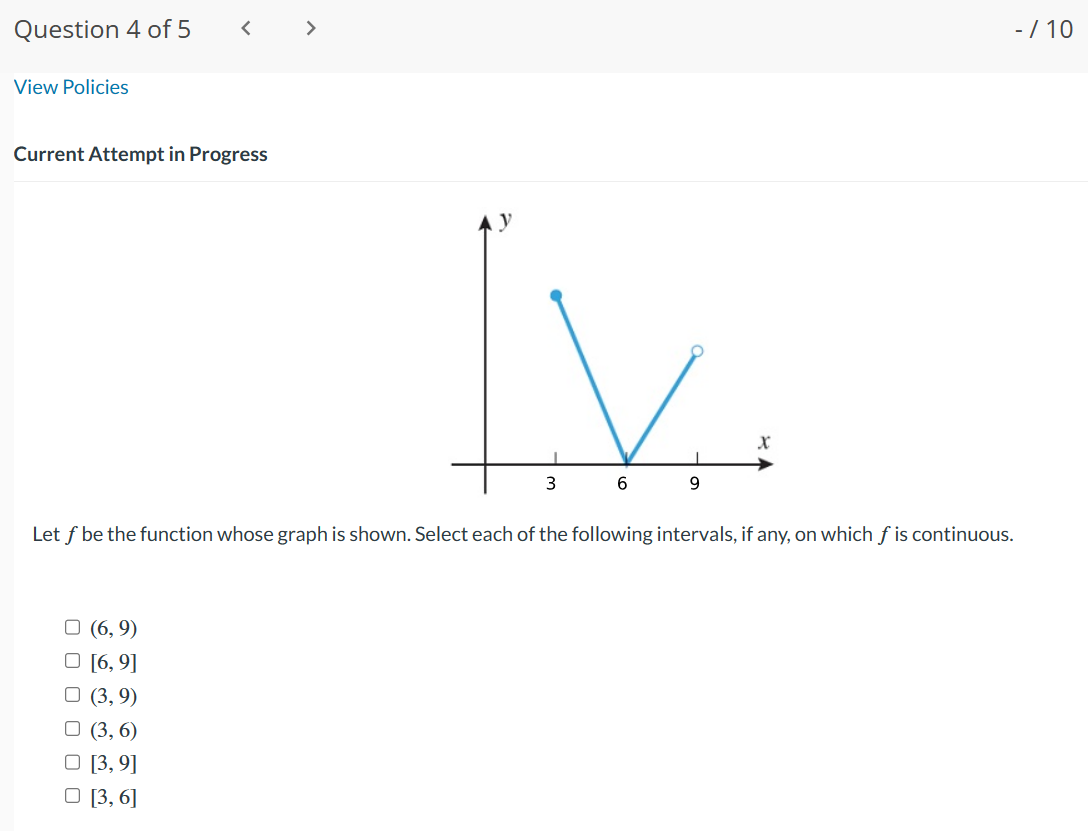
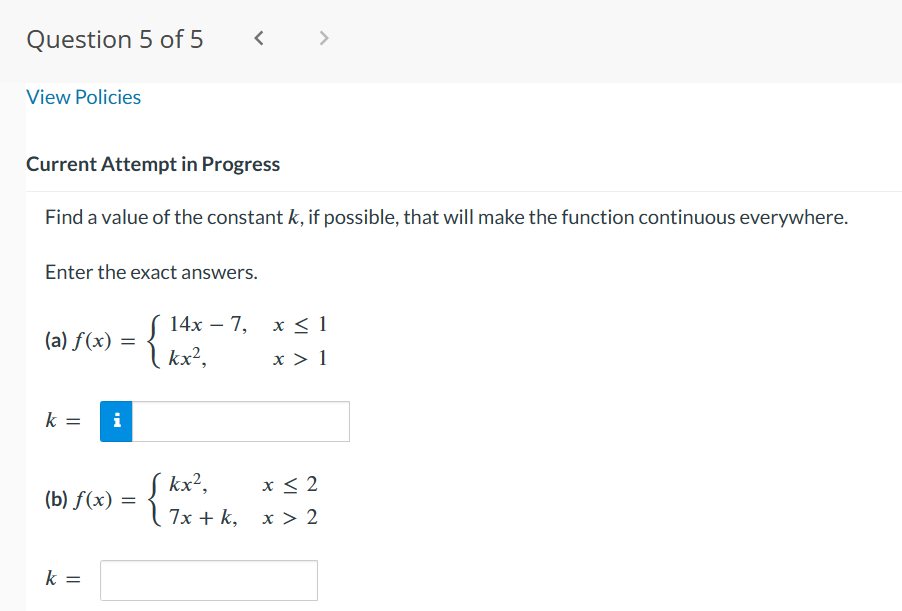
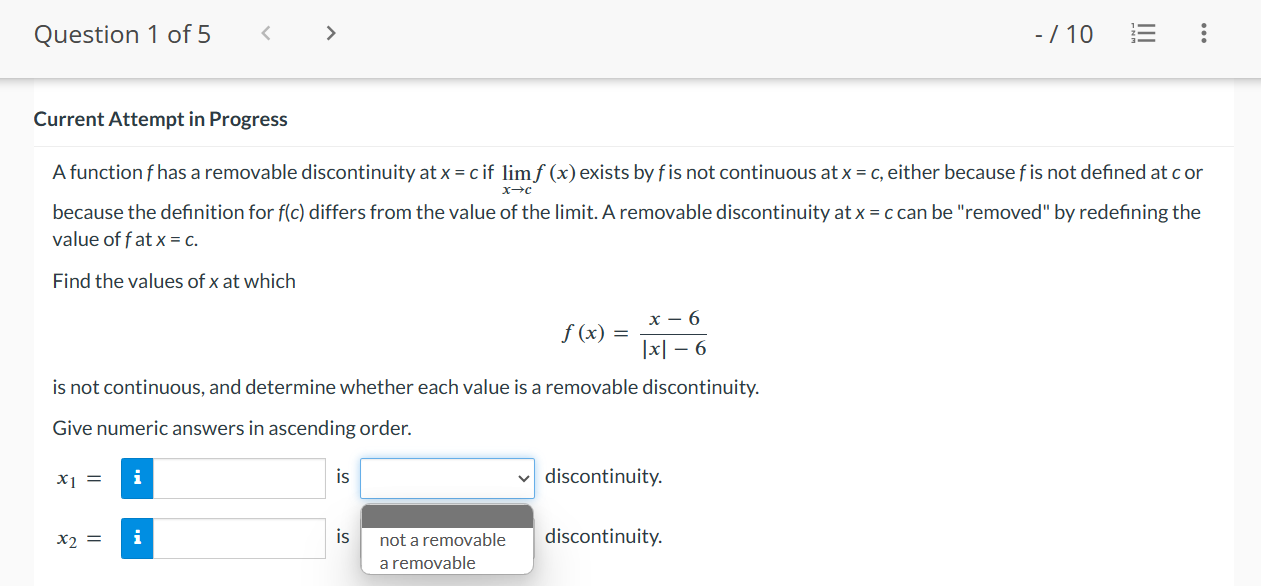
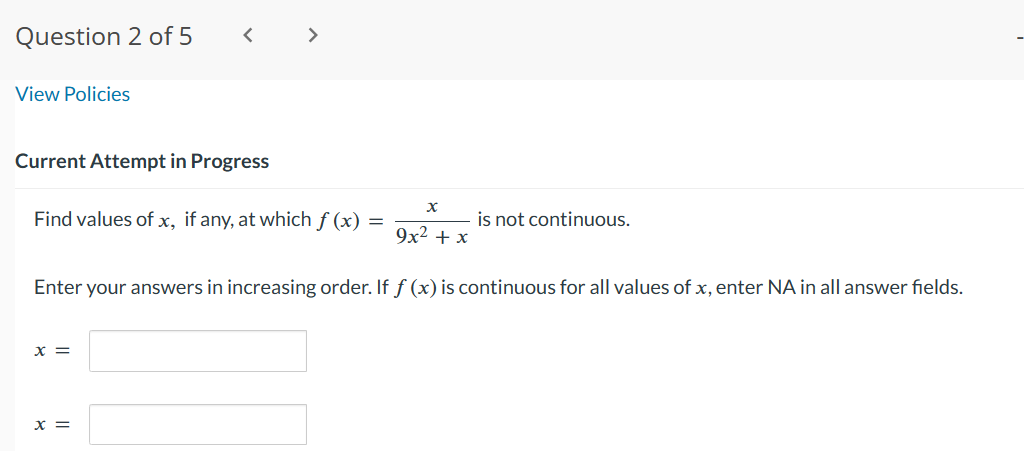
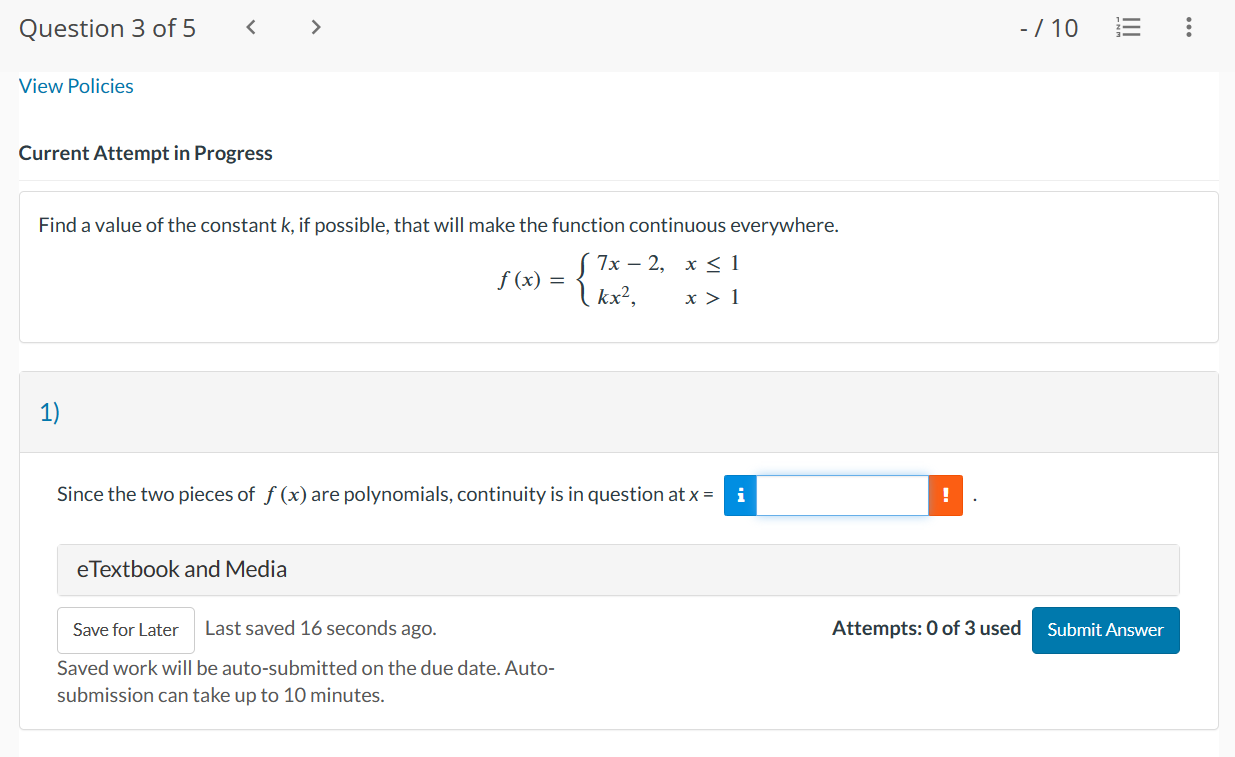
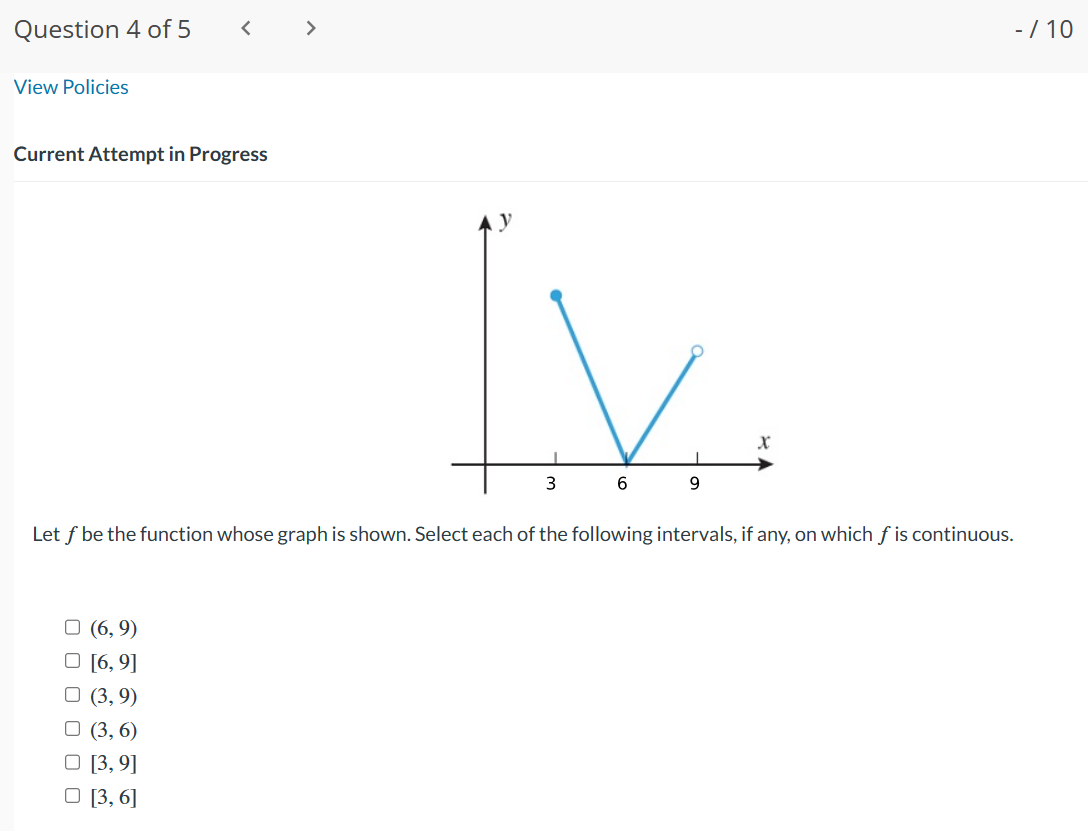
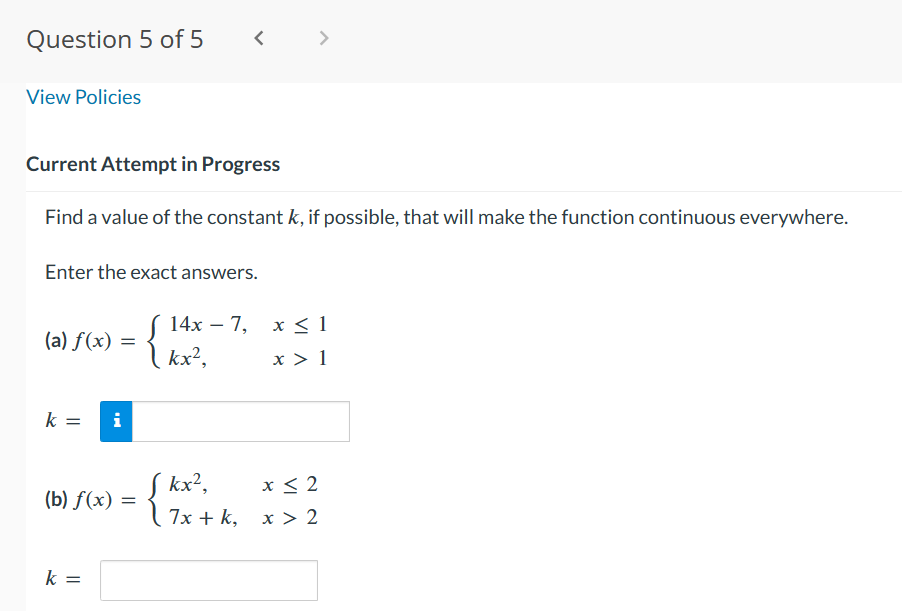
Question 1 of 5 - / 10 .. . Current Attempt in Progress A function f has a removable discontinuity at x = cif lim f (x) exists by f is not continuous at x = c, either because f is not defined at c or X- c because the definition for f(c) differs from the value of the limit. A removable discontinuity at x = c can be "removed" by redefining the value of fat x = C. Find the values of x at which f ( x ) = x - 6 |x - 6 is not continuous, and determine whether each value is a removable discontinuity. Give numeric answers in ascending order. X1 i is discontinuity. X2 = is not a removable discontinuity. a removableQuestion 2 of 5 > View Policies Current Attempt in Progress Find values of x, if any, at which f (x) = X is not continuous. 9x2 + x Enter your answers in increasing order. If f (x) is continuous for all values of x, enter NA in all answer fields. X = X =Question30f5 -/'|0 E View Policies Current Attempt in Progress Find a value of the constant k, if possible, that will make the function continuous everywhere. 7x2, x51 f(x){ kxz, x > 1 1} Since the two pieces of f(x) are polynomials, continuity is in question at x = :l . eTextbook and Media Save for Later Last saved 16 seconds ago. Attempts: O of 3 used Saved work will be auto-submitted on the due date. Auto- submission can take up to 10 minutes. Question4of5 -/ 10 View Policies Current Attempt in Progress Let f be the function whose graph is shown. Select each of the following intervals, if any, on which f is continuous. C] (6, 9) C1 [6, 9] C] (3,9) C] (3,6) [I] [3,9] C1 [3, 6] Question 5 of 5 l E .leZ x2 k