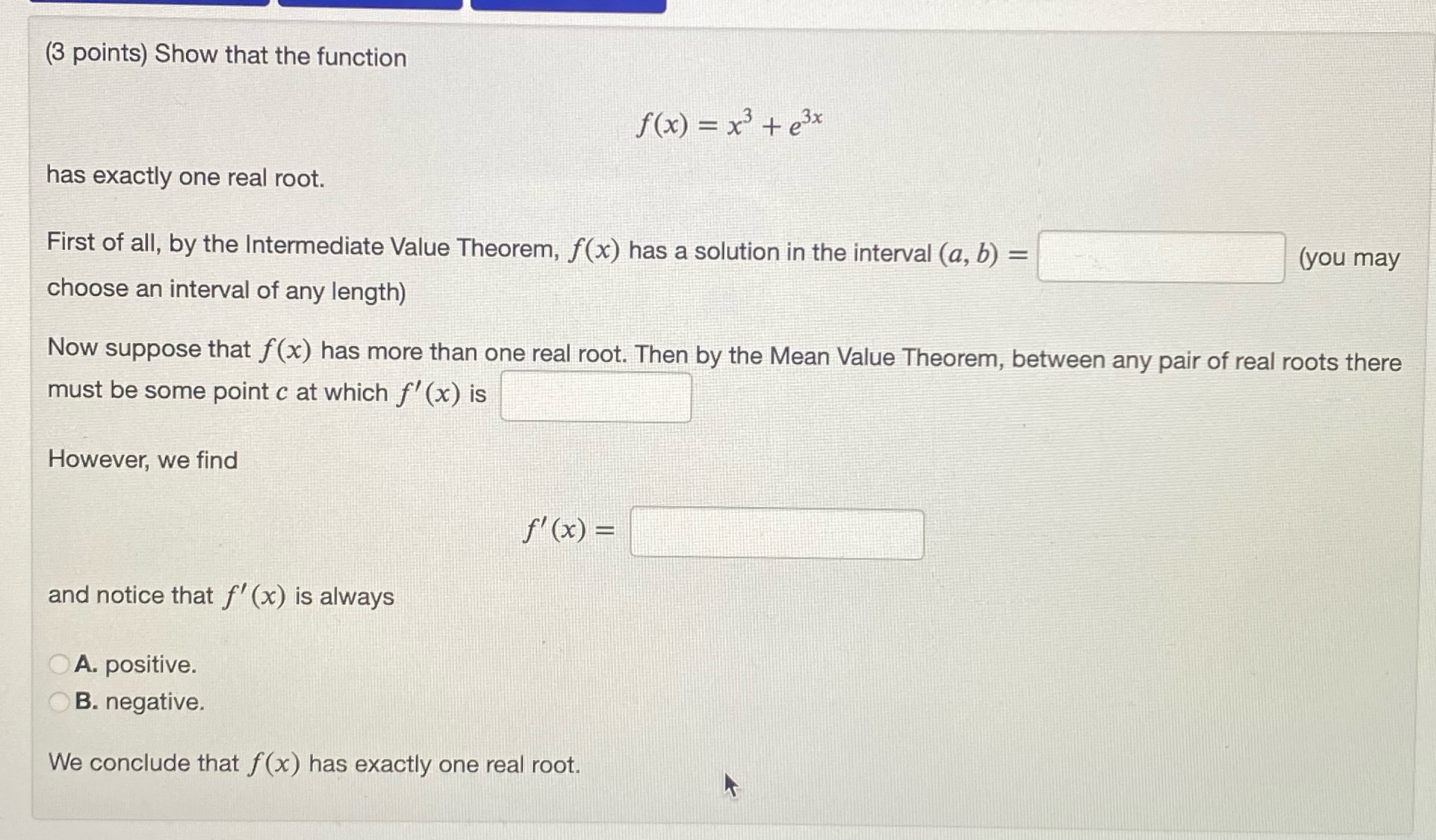
Question: note: answer the question in text form with little to no explanation (3 points) Show that the function f(x) = x3 +e3x has exactly one
note: answer the question in text form with little to no explanation
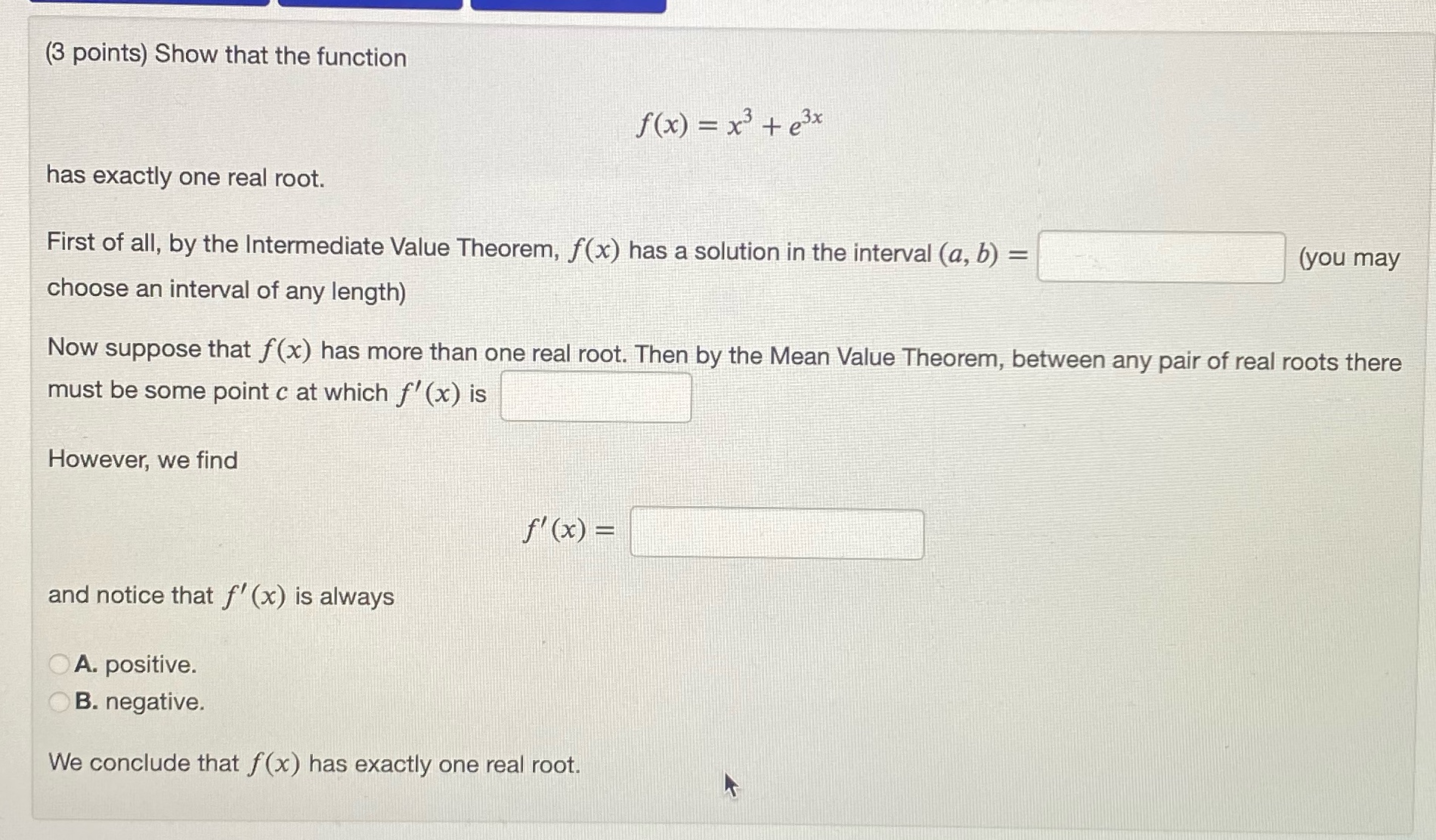
(3 points) Show that the function f(x) = x3 +e3x has exactly one real root. First of all, by the Intermediate Value Theorem, f(x) has a solution in the interval (a, b) = (you may choose an interval of any length) Now suppose that f(x) has more than one real root. Then by the Mean Value Theorem, between any pair of real roots there must be some point c at which f' (x) is However, we find f' ( x ) = and notice that f' (x) is always A. positive. OB. negative. We conclude that f(x) has exactly one real root
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


