Note: B0= 800

B1= -80

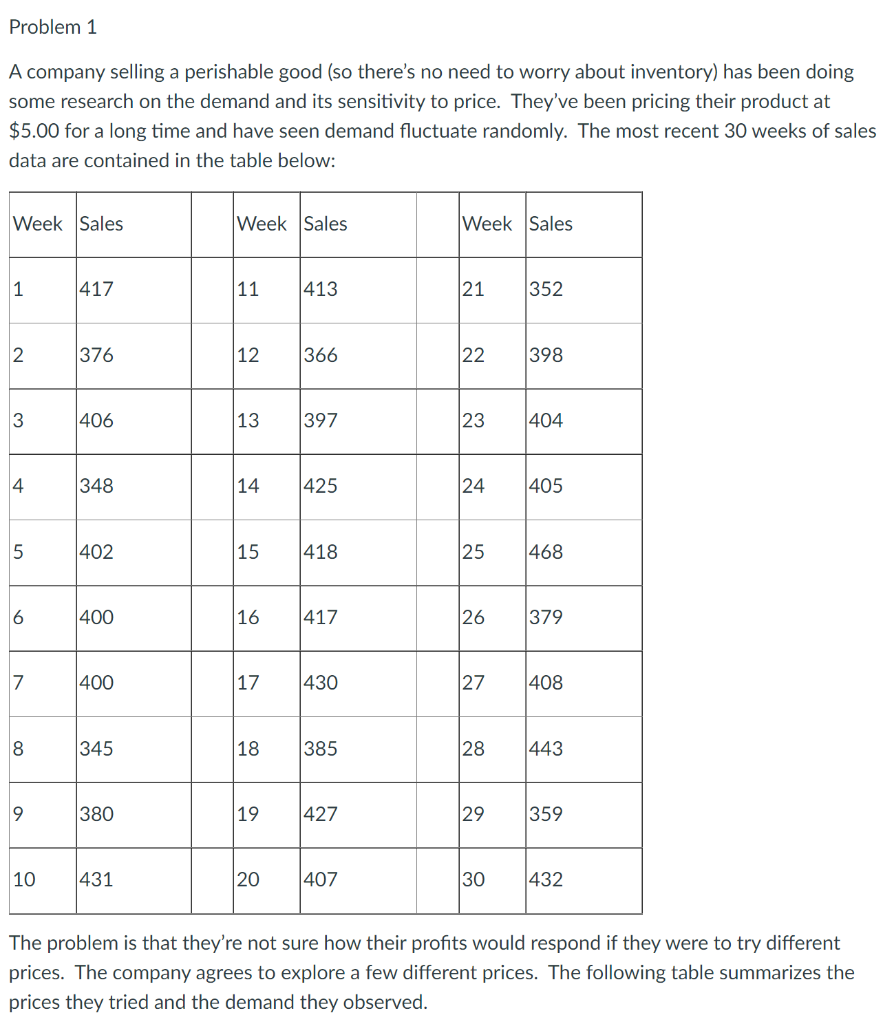
Problem 1 A company selling a perishable good (so there's no need to worry about inventory) has been doing some research on the demand and its sensitivity to price. They've been pricing their product at $5.00 for a long time and have seen demand fluctuate randomly. The most recent 30 weeks of sales data are contained in the table below: Week Sales Week Sales Week Sales 1 417 11 413 21 352 2 376 12 366 22 398 3 406 13 397 23 404 4 348 14 425 24 405 5 402 15 418 25 468 6 400 16 417 26 379 7 400 17 430 27 408 00 345 18 385 28 443 9 380 19 427 29 359 10 431 20 407 30 432 The problem is that they're not sure how their profits would respond if they were to try different prices. The company agrees to explore a few different prices. The following table summarizes the prices they tried and the demand they observed. Price Observed Demand $4.00 494 $6.00 344 In such a small price window, it's generally safe to assume that the demand is a linear function of the price with an additive stochastic element with a mean of zero: demand = Bo + B1 price te To understand how to properly price and supply their product, the company needs to know the mean and standard deviation at all prices. Your current task is to find the estimates, , and 1, that minimize the sum of squared residuals. What is the estimate of the slope (@1) that minimizes the sum of squared residuals